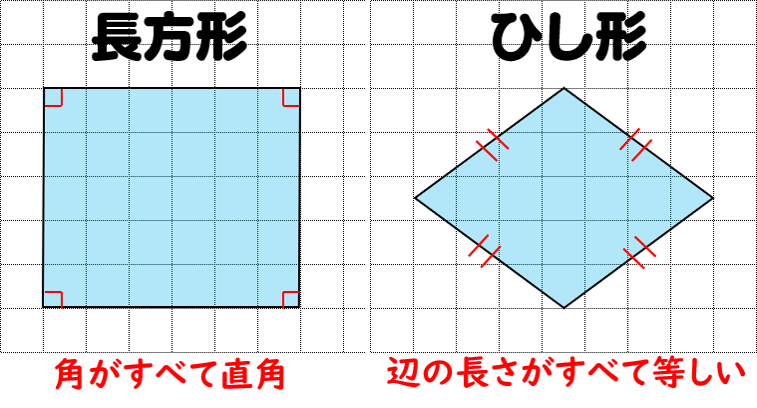
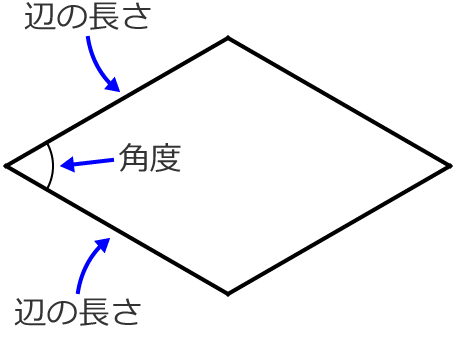
ただし、法面保護用に使用するひし形金網については受渡当事者間の規定による。 ⑥角度 角度は、図1に示すように、列線の屈曲部の角度をいい、その角度は85°を標準とする。 ⑦線径と網目の組み合せ jis g 3552による。11・ひし形の性質を調 辺の並び方や長 べる。 さ,角の大きさ 本 に着目し,ひし 時 形の性質を理解 している。 12・ひし形のかき方を ひし形をかくこ 理解する。 とができる。 13・対角線の意味を知 いろいろな四角 り,いろいろな四 形の対角線の特三角形の内角と外角 $ ABC$ において,$\angle A,\angle B,\angle C$ を,$ ABC$ の内角といいます. また,下図の $\angle ACD$ や $\angle BCE$ のように,一つの辺とその隣の辺の延長がつくる角を,外角といいます. さて,三角形の内角と外角について,次の重要な事実が成り立ちます.
図形 正五角形の分解 父ちゃんが教えたるっ
ひし形 角度 和
ひし形 角度 和-ひし形は平行四辺形の仲間??? 3分でわかる!ひし形(菱形)の定義 教科書によると「ひし形の定義」は、 4つの辺がすべて等しい四角形 だ。札幌市教育委員会(小学校4年生算数 令和2年10 月1日発行) かして点エの位置を決める。 1組の向かい合う (下の表に 四辺形 台形 平行 四辺形 ひし形 長方形 正方形 2本の対角線の長さは等しい 2本の対角線が交わった点でそれぞれ




図形の角度 四角形 小5 小6 プリントok
図形 定義・定理 まとめ 対頂角 𝟖は等しい 直線の角度 ° 平行線の 同位角 𝟖 は等しい 角形の内角の和 °×(𝒏− ) 平行線の 多角形の外角の和錯角 𝟔は等しい ° 同位角 が等しければ、2直線は平行 〇 合同な図形の対応する線分や角は等し台形,平行四辺形,ひし形 (1)台形と平行四辺形 右の平行四辺形で,辺アイ,アエはそれぞれ何cmでしょう。 また,角ア,ウ,エの角度はそれぞれ何度でしょう。 角ウ (2)ひし形 向かい合った1組の辺が平行な四角形を といいます。第2レベル ・三角形や四角形の内角の和を利用して,角の大きさを求めることができ る。 ・既習の図形について,角度を表すことができない。 12人 第1レベル ・三角形の内角の和を利用して,角の大きさを求めることができる。
例えば、図のような2つのひし形を考えてみます。 辺の長さは同じですが、面積は全く異なります (片方はつぶれていて面積が小さい、片方は正方形に近くて面積が大きい)。 一辺の長さだけでなく他の情報(角度など)が分かれば面積を求めることができます。直線図形 (入試問題) → 携帯版は別頁 == 直線図形と角 == (入試問題) 要点 (1) 三角形の内角の和は180°に等しい. (2) 三角形の外角は,それと隣り合わない2つの内角の和に等しい. ≪例≫ (1) 上の図において ∠A∠B∠C=180° (2) 上の図において ∠ACDひし形の面積の公式 ひし形の面積は 2 2 つの対角線の長さをかけて2で割ったもの、つまり 『対角線×対角線÷2 ÷ 2 』 で求めることができます。 平行四辺形の一種でもあるので、底辺と高さが分かっていれば『底辺×高さ』でも求められます。 たとえば
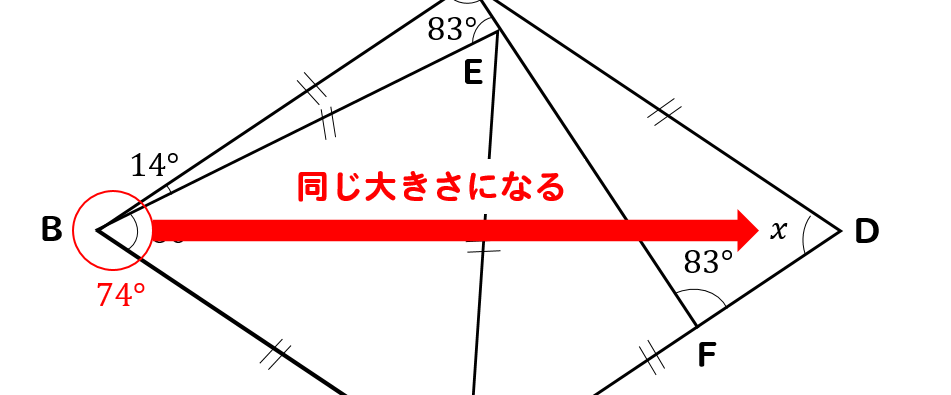
再入荷!アジアン照明 間接照明 アジアン家具 バリ雑貨でアジアンインテリア バリ リゾート フロアスタンドライト おしゃれ バリ風インテリア。あす楽アジアン雑貨 スタンドライトひし形100cm オリエンタル 照明 LED対応 アジアンランプ バリ雑貨 フロアライト 和 ジャパニーズ バリ 渋谷教育学園幕張中角度の和 19年 4年生 5年生 6年生 入試解説 千葉 渋谷 男子校 角度 角度の和 ★★★★☆☆(中学入試難関校レベル) 印象に残った入試問題の良問を「今年の1問」と題して取り上げています。 志望校への腕試しや,重要項目の確認に答 ひし形 ※ 4 つの直角三角形 \triangle \rm ADQ , \triangle \rm CDS , \triangle \rm EFQ , \triangle \rm GFS は合同なので, \rm DQ=DS=FQ=FS なお, ひし形は, 長方形のように 2 つの対角線の長さが等しいとは限りません 実際, \rm DF\not=QS です
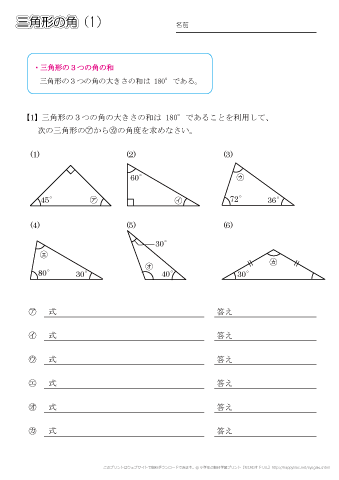



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生



ひし形の定義は 1分でわかる定義 正方形 平行四辺形との違い 対角線との関係
ひし形 面積問題 小学5年生 ひし形とは、4つの辺の長さがすべて同じになります さらに、対角線が必ず90°で交わります ひし形の面積は、 公式 対角線×対角線÷2 垂直に交わる線の横と縦を掛けそれを2で割ってください和 〔 〕 差〔 〕 和 〔 〕 差〔 〕 3 右の図で,直線アと直線イは平行です。 (2点×3) ⑴ あの角度は何度ですか。 〔 〕 ⑵ いの角度は何度ですか。 〔 〕 ⑶ うの角度は何度ですか。 〔 〕 4 右の図はひし形ひし形の性質を理 解する。 ・定義や性質をもと に、ひし形のかき方 を考える。 ・対角線の意味と用 語を理解する。 ・対角線から四角形 を考察して、理解 を深める。 (対角線の交わる位 置や長さ、垂直か どうかなど) ・平行四辺形、ひし形、 台形で




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ




小学生 平行四辺形と長方形のちがいは Active Learning 学院
ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積二等辺三角形の角度の求め方 厳選6問解説!←今回の記事 正三角形の角度 正方形、ひし形との融合問題を解説! 平行四辺形とひし形の違いってなに?? 平行四辺形の角度、辺の長さを求める問題を解説 事実として4つの角度が分かっている四角形と角度が分からない四角形Aを提示し、どんな四角形も内角の和が360°であるといえるか問いかける。 四角形の4つの角の大きさの和が何度になるか調べて説明できるようになろう。 わ か る
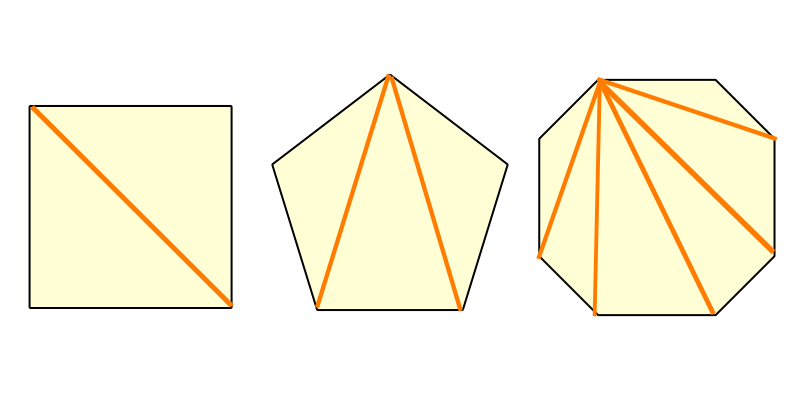



多角形の内角の和 簡単に計算できる電卓サイト




四角形の英語 正方形 長方形 台形 ひし形 平行四辺形など 英語独学マスター
3 四角形の内角の和 は360°であること を理解し,計算で四 角形の角の大きさ を求めることがで きる。 ・角度を測らないで,四角形の四 つの内角の和を求める方法を 考える。 ・各自の考えた求め方について発 表し,検討する。 考三角形の内角の和を基にの角の大きさの和は、 180×3=540で、540°になる。 1四角形の4つの角の大きさの和は 360°であることを利用して、 次の四角形の㋐~㋕の角度を求めなさい。 多角形をいくつかの三角形や四角形に分けると、 角の大きさの和を求めることができる。平行四辺形,ひし形について理解し,図形についての見方や感覚を豊かにする。 内容 C 図形 レディネステストから,角度に関する理解は100%であり,しっかり理解できていた。 ・多角形の内角の和
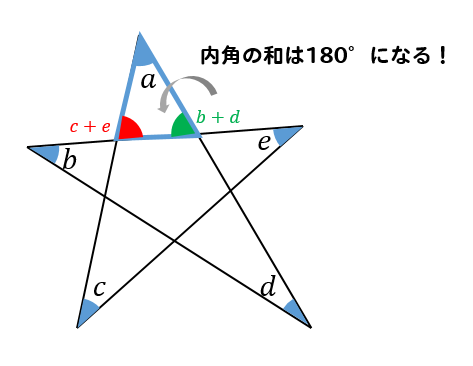



星形の角度 内角の和の求め方を問題解説 数スタ



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun
平行四辺形,ひし形について理解し,図形についての見方や感覚を豊かにする。 この要素は,第5 学年で学習する四角形の内角の和や 第1 時で作成したドットカードは,辺の長さや角度に注目した弁別学習のときだけでなく,垂直 ひし形(菱形)の定義 をわかりやすく解説していくよ。 よかったら参考にしてみてね^^ 〜もくじ〜 菱形の定義;正多面体 正4面体,正6面体,正8面体,正12面体,正面体はプラトン(紀元前)の著作に現れることからプラトンの正多面体と呼ばれます.正面体と正12面体には黄金比が関係しています. 正多面体とは,1) 凸多面体(有限個の平面で囲まれる領域




中2数学 長方形 ひし形 正方形 練習編 映像授業のtry It トライイット




小学校5年 算数 四角形の内角の和 Youtube
対角線aが2、対角線bが3のひし形の面積・周囲の長さ・角度 面積 S:3 周囲の長さ L: 角度 A: 角度 B: 四角形の面積(4辺と対角の和)再入荷!アジアン雑貨バリ雑貨でアジアンインテリア フロアライト バリ おしゃれ 照明 アジアンリゾート 間接照明 バリ島。アジアン雑貨 スタンドライトひし形150cm 照明 サンダルウッド&コットン&バナナリーフ オリエンタル 海外インテリア バリ雑貨 フロアライト 和 バリ おしゃれなかま分けし、ひし形の意味を 知る。 ・辺の長さやならび方、角度などに着目し、 四角形の仲間分けをしている。(考) ・ひし形の意味を知る。(知) 11 ひし形の性質を調べる。 ひし形のかき方を考える。 ・ひし形の性質を理解している。(知)



菱形と長方形はどちらが美しいですか Quora
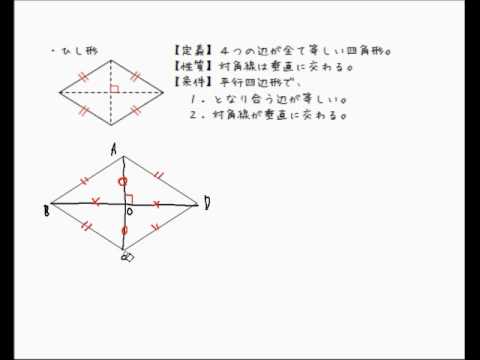



ひし形の定義 性質 条件 Youtube
平行四辺形・長方形・ひし形・正方形は、実はどれも台形の一種と言えますね。 角度についても、台形の性質を利用すれば簡単に求められますね。 台形の性質1「錯角の和が180度になる」とあるが、角aと角dのような関係を錯角とは言わない。角aと 多角形(四角形・五角形・六角形・・・)の内角の和の公式&問題の解き方 管理人 10月 6, 18 / 11月 18, 18 そしてその中でもさらに多角形の内角の角度に関する問題は頻出されま四角形の内角の和を考えるときは 長方形や正方形で考えるのが簡単だと思います。 長方形や正方形は全ての角度が90度ですから、 それが4個あるので 90度×4=360度 となります。とても簡単ですよね? しかし これだと面白くないので少し違う考え方をし



正三角形の角度 正方形 ひし形との融合問題を解説 数スタ
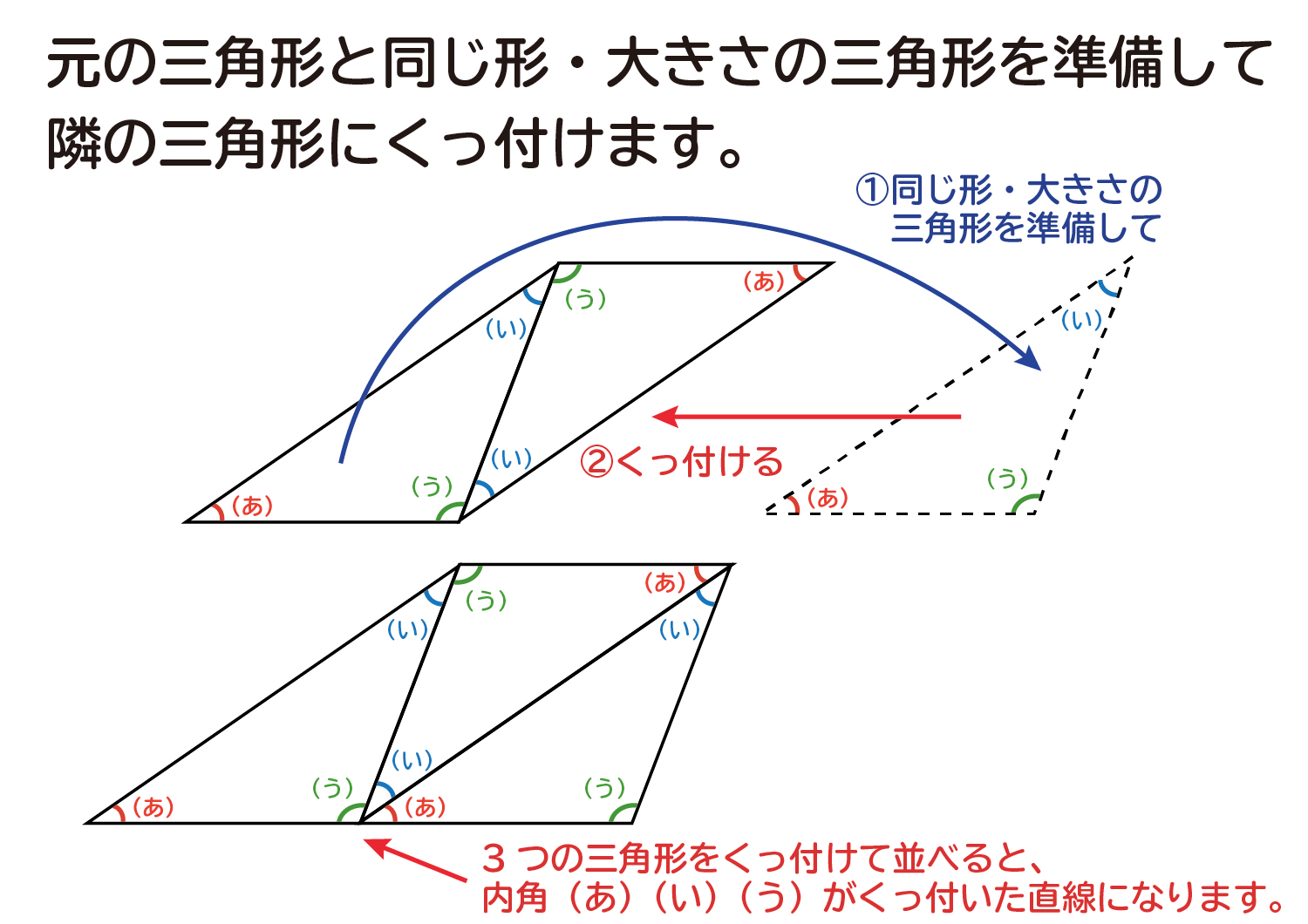



なぜ 三角形の 内角の和は180 なのか を説明します おかわりドリル
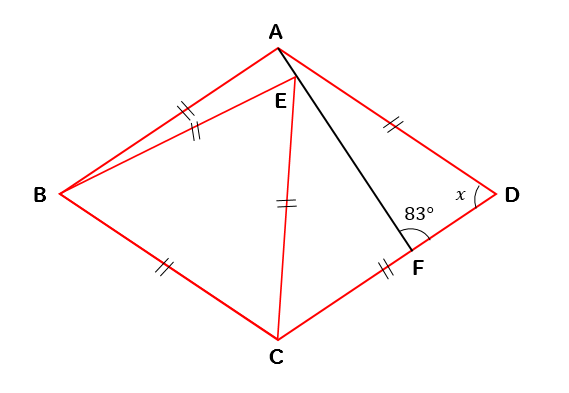
第219問 正三角形とひし形 図形ドリル ひし形 二等辺三角形 正三角形 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~! ! 」と言いそうな良問を。 受験算数の定番からマニアックな問題まで。 図形ドリルでは,色々なタイプの図形問題を(令和2年4月1日付け) 最大は、正12角形の 3(2√3)≒ で、最小は、一辺が3のひし形をつくればいく らでも0に近くできますので、作れる面積の範囲は、0<(面積)≦3(2√3) です。内角の和 180° 360 7° 900° 1080° 1260° ・・・ ° (三角形の内角の和×三角形の数が内角の和になるきまりを使っている。) (二十角形までの多角形の内角の和が180°ずつ増えるきまりを使っている。) ・九角形は1080°+180°で1260°です。



小学4年生の算数です 画像のひし形をコンパスを使って描く方法を教え Yahoo 知恵袋
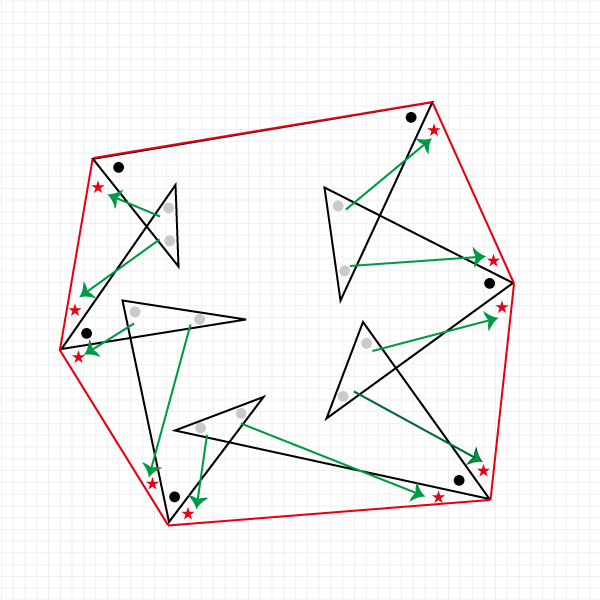



角度情報がない図形の合計の角度 星形多角形 受験算数入門
内角の和を考えて求める場合には 180 \times (102)=1440° 内角の和をこのように求めて 10で割ってやれば求めることができます。 1440 \div 10 =144° 1つの外角が40°の正多角形を答えなさい。 解説&答えはこちら \LARGE { {正九角形}} 1つ分の外角が40°になるという
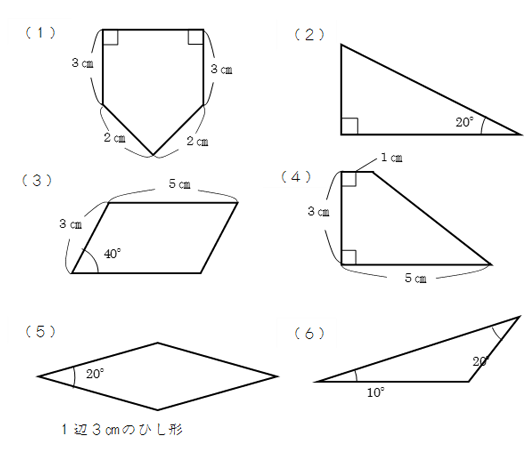



第22回 図形の切り分け いろいろな形に切る 算数ドクター




平行四辺形の辺や角を求める Youtube



ひし形の角度



Q Tbn And9gcqgkvh4ulvtqslh0feidoztdsmlu5sly8eyky9r6y9nixshzokx Usqp Cau




図形の角度 四角形 小5 小6 プリントok



Http Www Kochinet Ed Jp Shimizu E Kounaikensyuu H28tangenkoso5nen Pdf
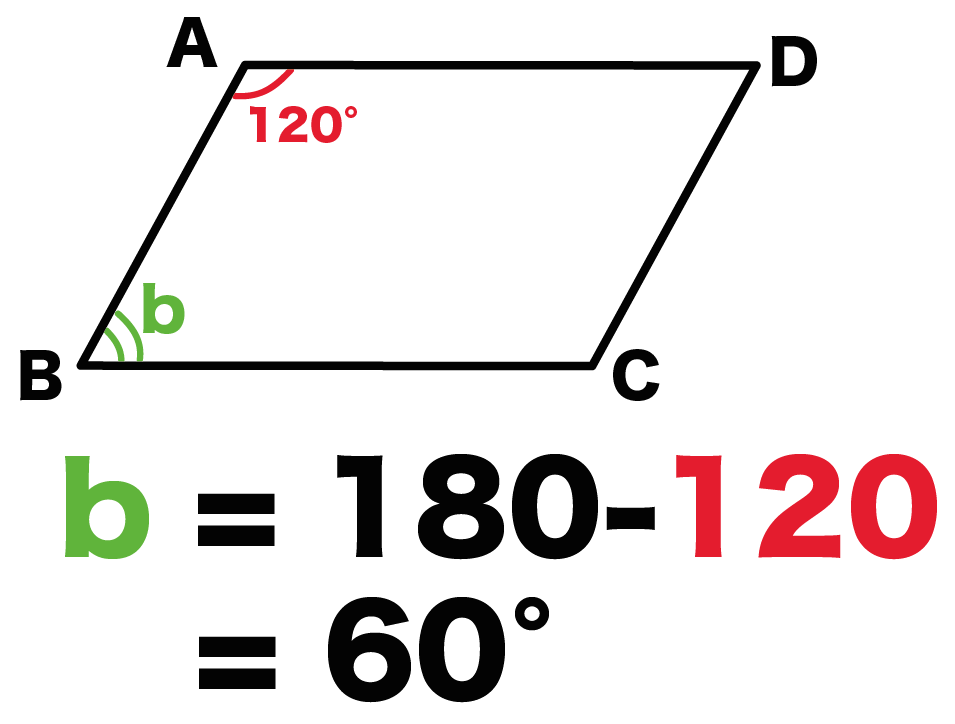



簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




図形の角度 四角形 小5 小6 プリントok



Http Www Sendai C Ed Jp 02kensyu 02cyoken H27 Yoshida S Pdf
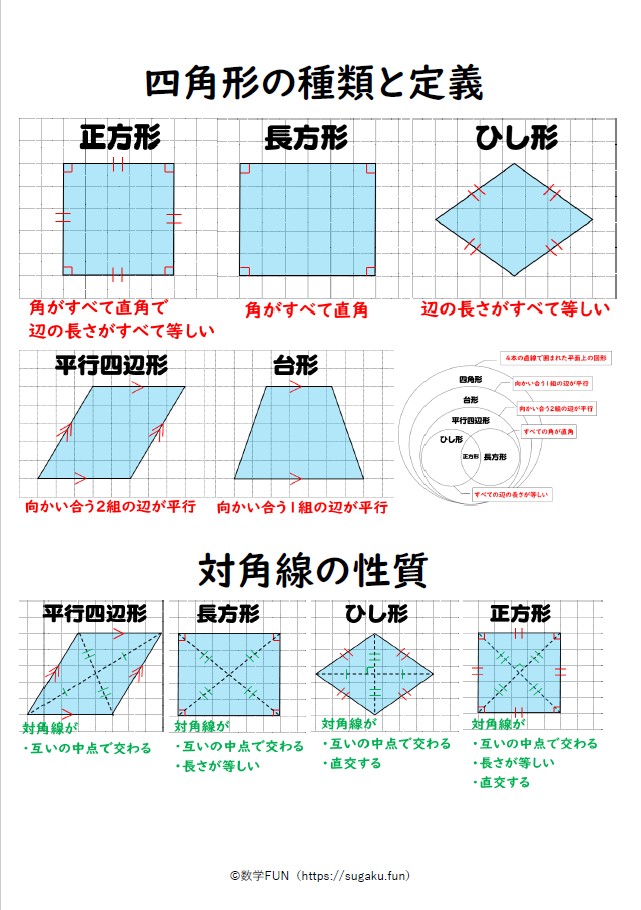



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun
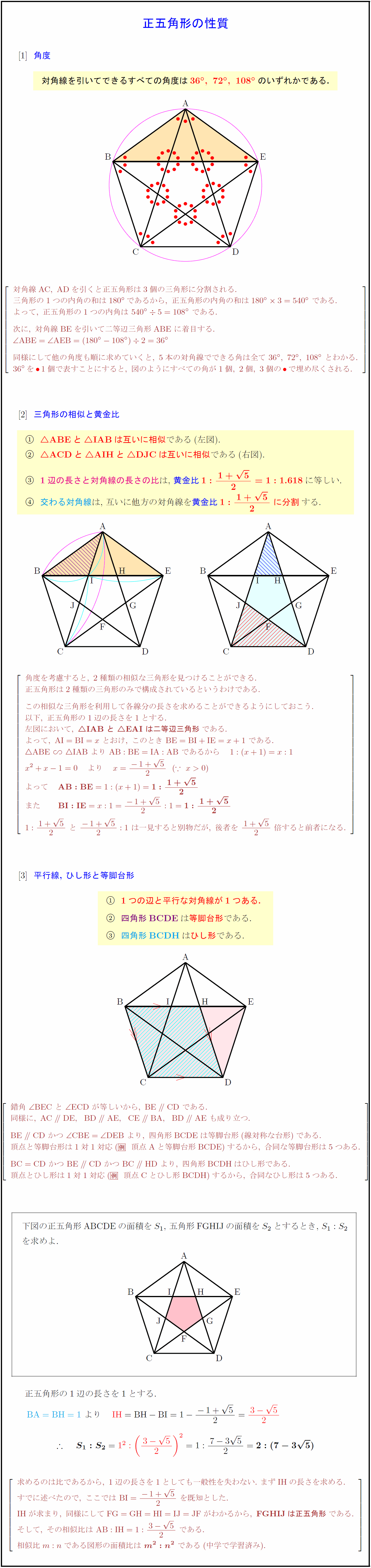



高校数学a 正五角形の性質 三角形の相似 黄金比 等脚台形 ひし形 受験の月



ひし形の定義は 1分でわかる定義 正方形 平行四辺形との違い 対角線との関係




高校数学b ベクトルと正五角形 Cos108 の値 受験の月



平面図形の角度 第28問 角度の和 浅野中学 03年 甲陽学院中学 02年 入試問題 算数 まいにち一題 中学受験過去問題研究
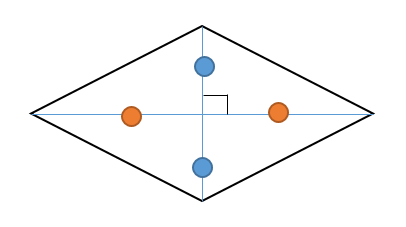



小学算数 平行四辺形 ひし形 長方形 正方形の対角線は真ん中で交わる 偏差値40プログラマー



ひし形の定義は 1分でわかる定義 正方形 平行四辺形との違い 対角線との関係
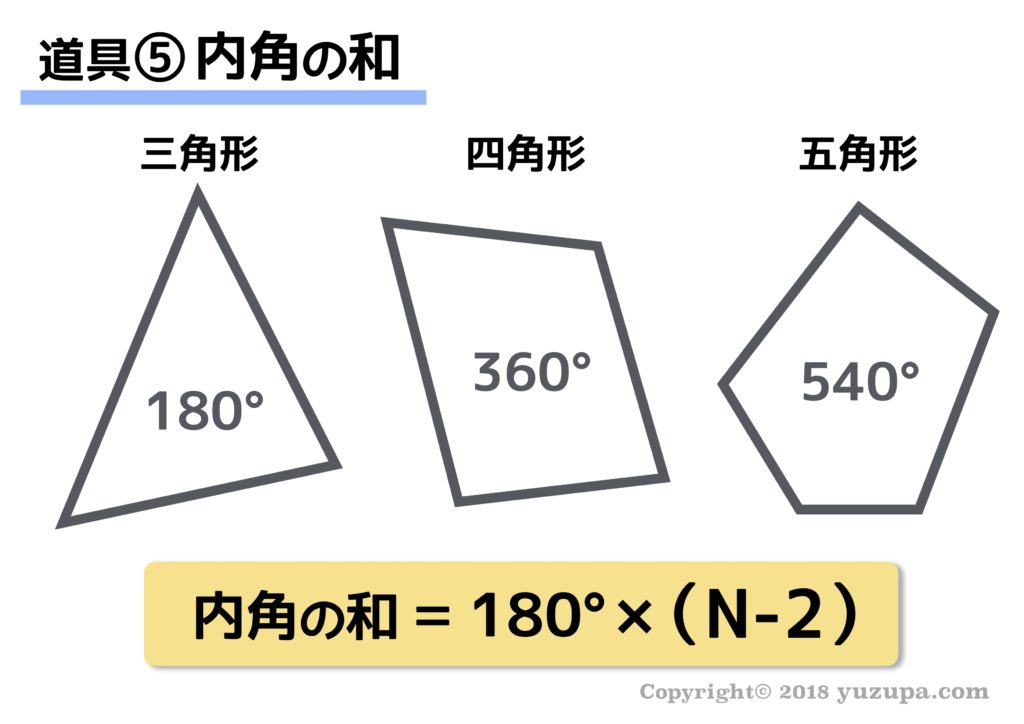



中学受験 図形の角度問題は 7つ道具 で攻略 かるび勉強部屋




簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
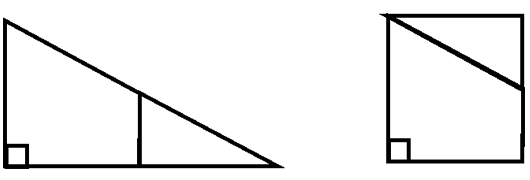



第22回 図形の切り分け いろいろな形に切る 算数ドクター



長方形の計算 もう一度やり直しの算数 数学
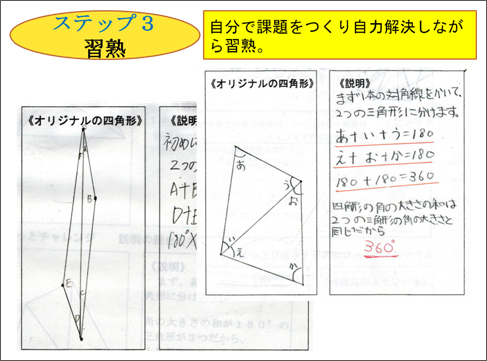



重なる形と図形の角を調べよう 図形の角と合同 第5学年 小学校 算数 My実践事例 日本文教出版




角度の解き方4つしかない説
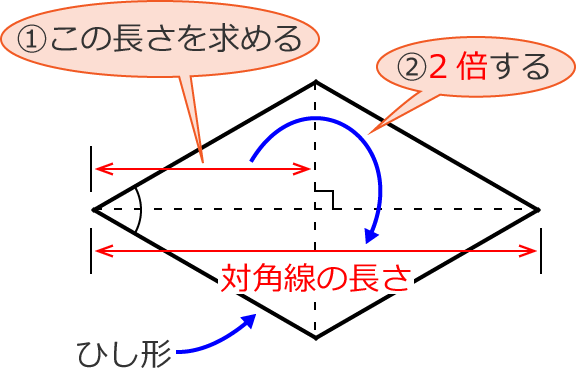



ひし形の対角線の長さの求め方



1
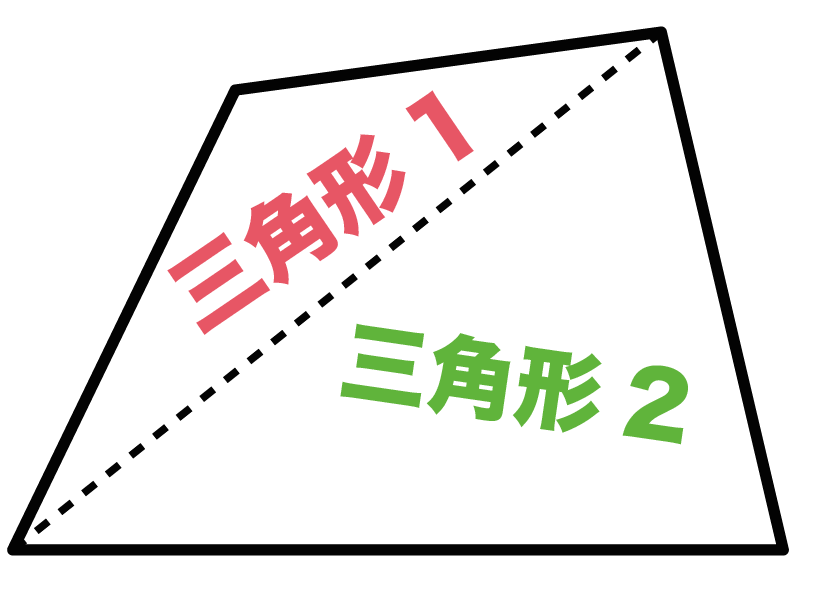



簡単公式 3秒でわかる 四角形の内角の和の求め方 Qikeru 学びを楽しくわかりやすく




至急 1問でもいいので教えて下さい よろしくお願いします Clear




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ



1
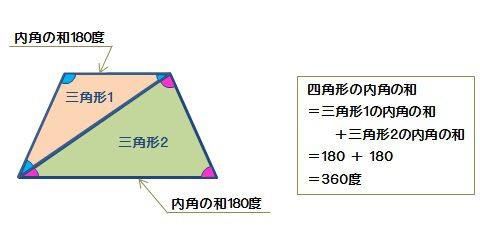



四角形の内角の和 算数の公式覚えてますか



ひし形の性質を教えて下さい 4つの角の大きさがみな等しいのはひし形 Yahoo 知恵袋



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



Q Tbn And9gctygkghqwdw3gq3qrgj51pa5x3j74rgia9vkgwdewbxneabh7zq Usqp Cau



ひし形の定義は 1分でわかる定義 正方形 平行四辺形との違い 対角線との関係



Http Www Ikushin Co Jp Shuppan Textimg 17matokan Chuhyo Sugaku Hon Pdf




平行四辺形の仲間を知ろう 電験3種web



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典
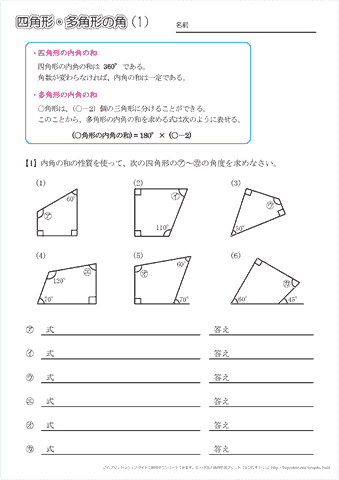



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生




無料の学習プリント 小学4年生の算数ドリル いろいろな四角形 みそにゃch



図形 正五角形の分解 父ちゃんが教えたるっ
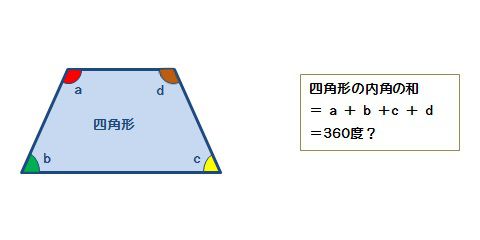



四角形の内角の和 算数の公式覚えてますか




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
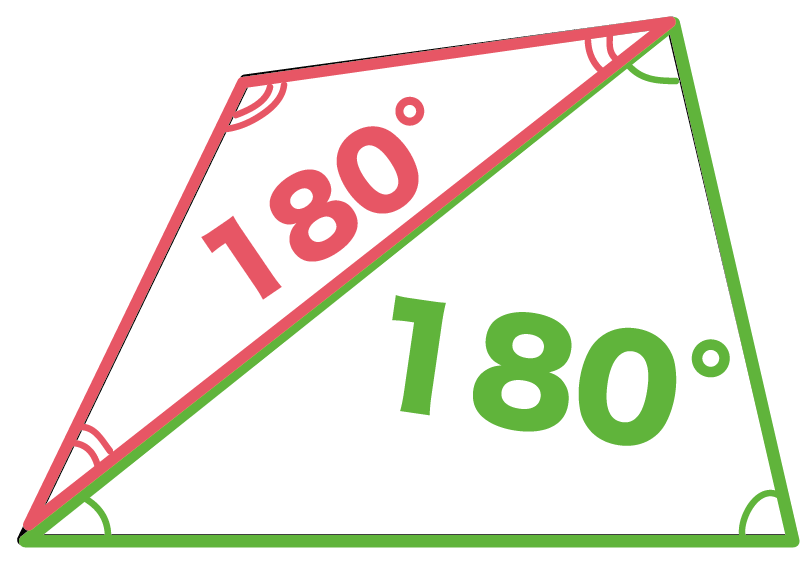



簡単公式 3秒でわかる 四角形の内角の和の求め方 Qikeru 学びを楽しくわかりやすく



図形の問題を得意にしたい
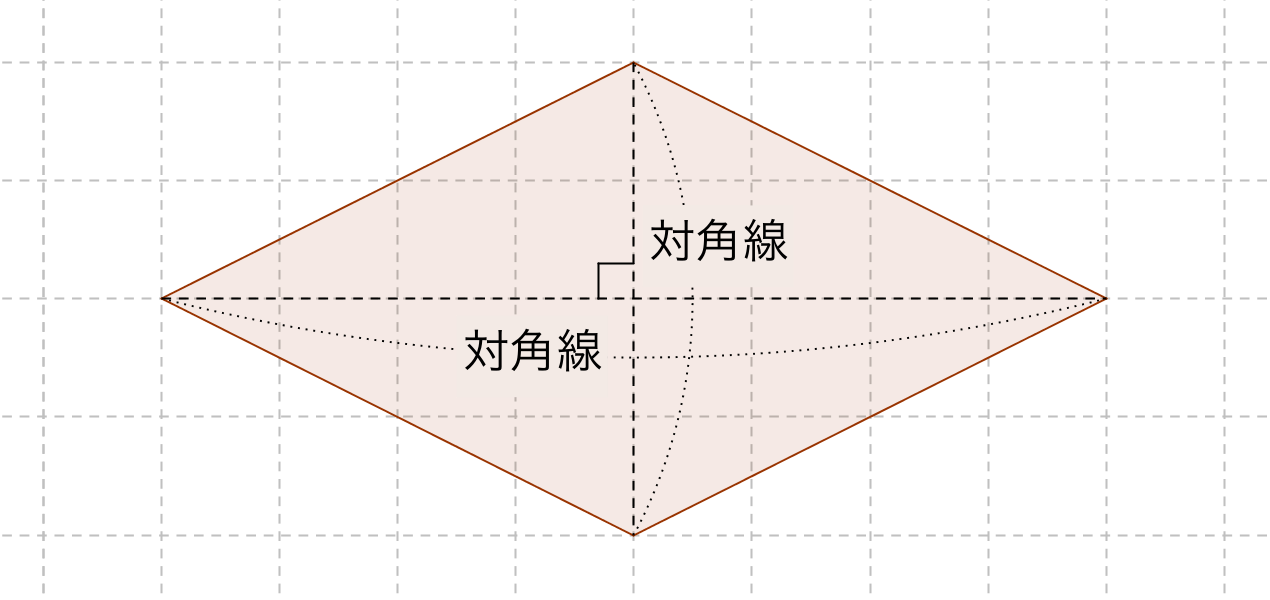



ひし形の面積の公式 算数の公式



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典




ひし形の面積の求め方 公式と計算例
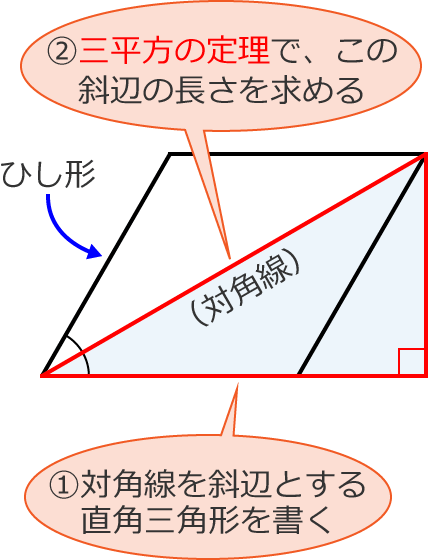



ひし形の対角線の長さの求め方



ひし形の対角線の長さの求め方



正三角形の角度 正方形 ひし形との融合問題を解説 数スタ




小学生 平行四辺形と長方形のちがいは Active Learning 学院




図形の角度 四角形 小5 小6 プリントok
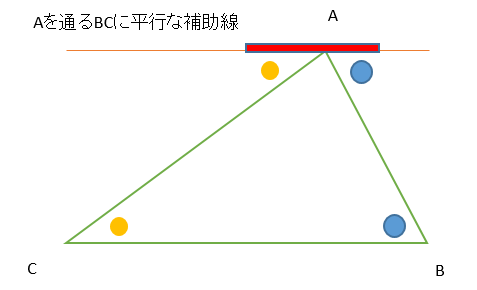



小学算数 幼稚園児でもわかる 三角形の内角の和 180度 の証明 偏差値40プログラマー



Www Shinko Keirin Co Jp Keirinkan Chu Math Support Data H27 Shidoupoint Sugaku Pdf



図形の問題を得意にしたい




ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
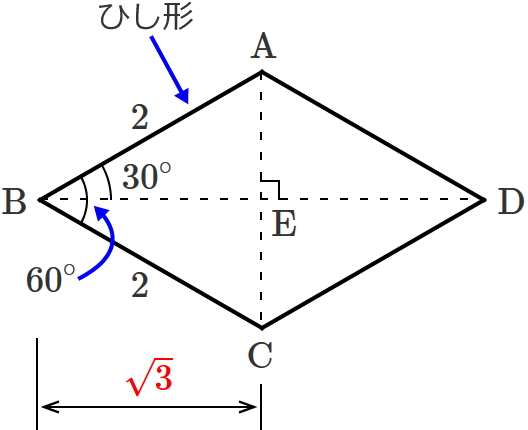



ひし形の対角線の長さの求め方



画像 ひし形 の 書き方 小 4 シモネタ
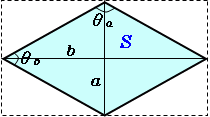



ひし形の面積 高精度計算サイト
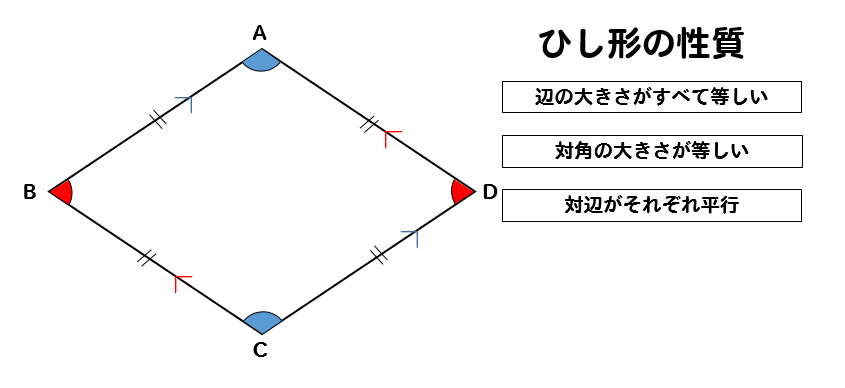



正三角形の角度 正方形 ひし形との融合問題を解説 数スタ
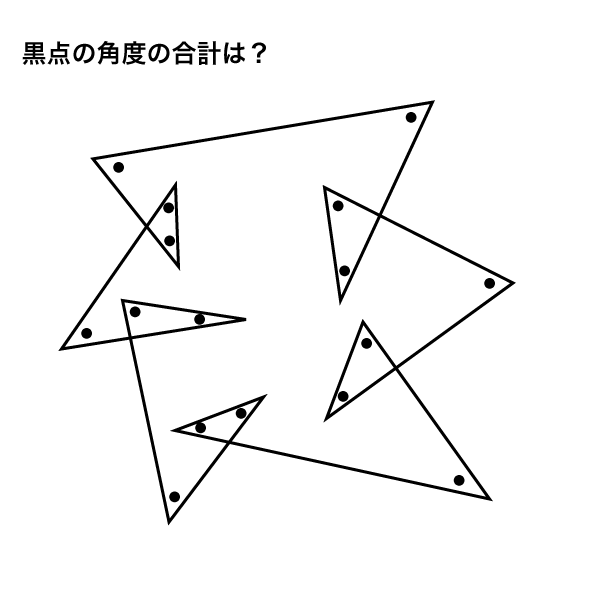



角度情報がない図形の合計の角度 星形多角形 受験算数入門
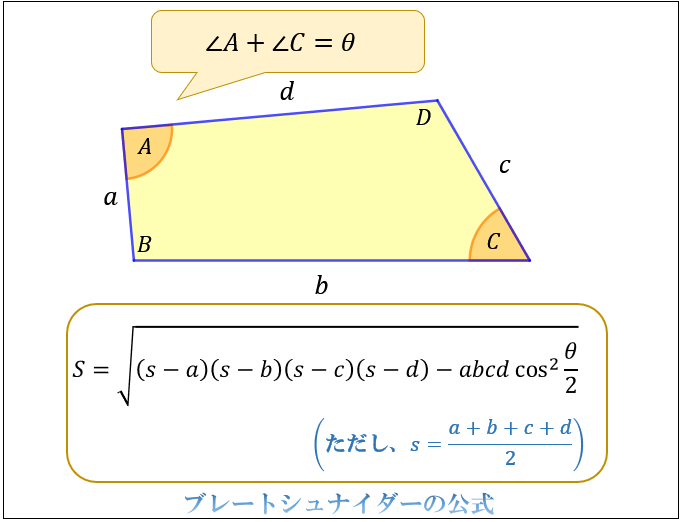



四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



Http Kylaboratory Com Wp Wp Content Uploads 18 10 17f60aa7f52cdd6a27f9d7ef858 1 Pdf




世界一分かりやすい算数 小5 合同な図形
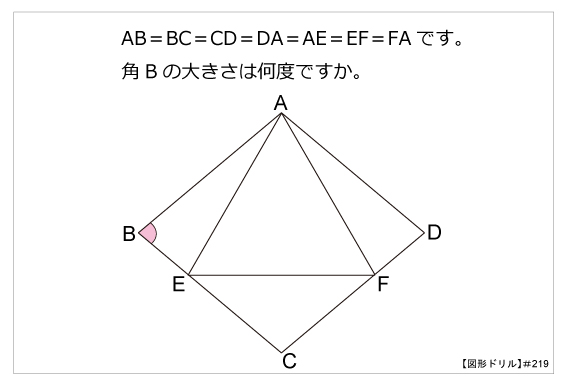



図形ドリル 第219問 正三角形とひし形 算数星人のweb問題集 中学受験算数の問題に挑戦
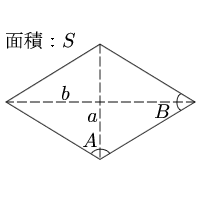



ひし形 面積の計算 計算サイト
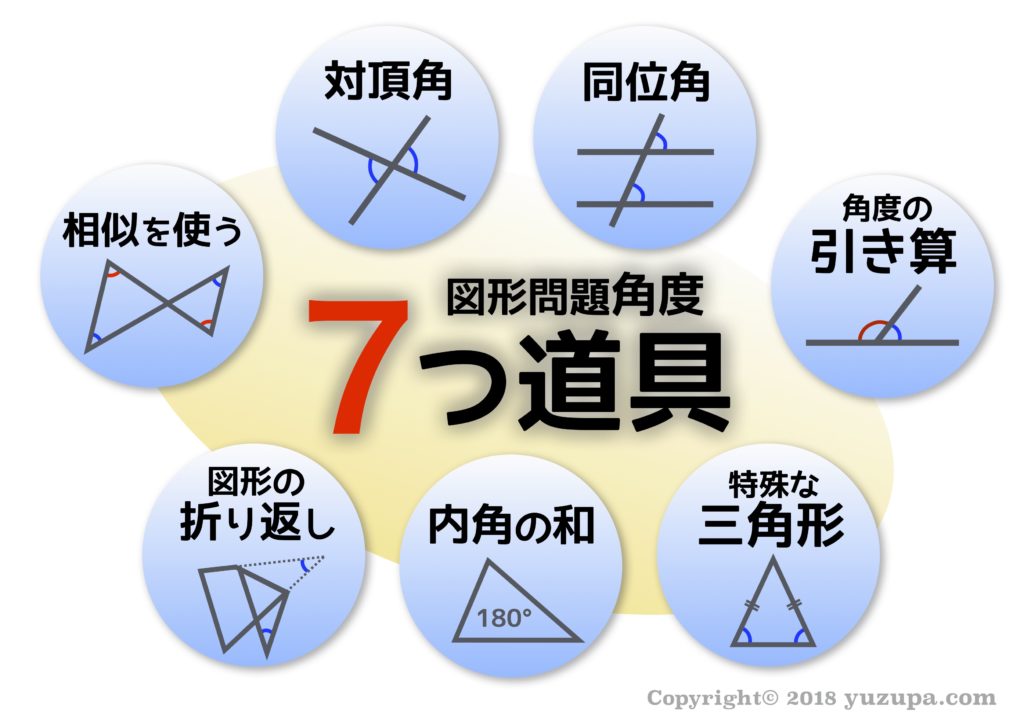



中学受験 図形の角度問題は 7つ道具 で攻略 かるび勉強部屋



図形の問題を得意にしたい




星形の角度 内角の和の求め方を問題解説 数スタ



ひし形の性質を教えて下さい 4つの角の大きさがみな等しいのはひし形 Yahoo 知恵袋



フレッシュ ひし形 書き方 コンパス



図形 正五角形の分解 父ちゃんが教えたるっ
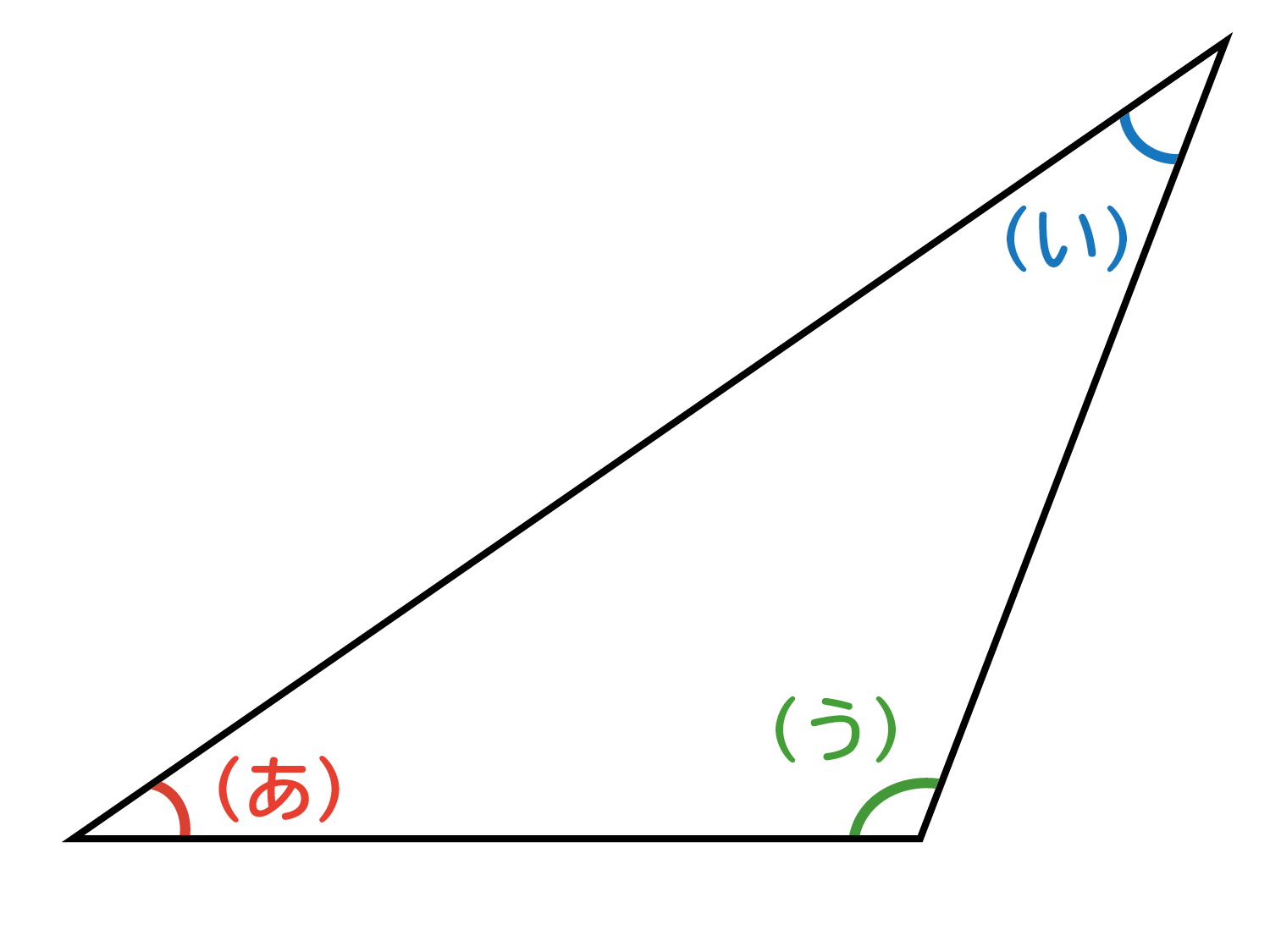



なぜ 三角形の 内角の和は180 なのか を説明します おかわりドリル




至急 1問でもいいので教えて下さい よろしくお願いします Clear



中学から数学だいすき




十五角形 Wikipedia



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典




ひし形の面積の求め方 公式と計算例




簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




角度 3 図形問題 算数 多角形 和 中学受験 桐光学園中学校 勉強 Youtube スタディチューブ
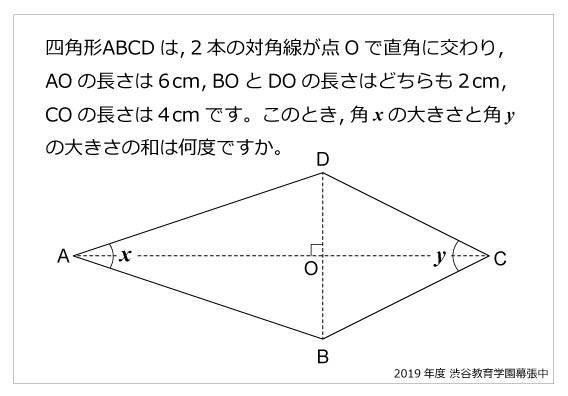



今年の1問 19年渋谷教育学園幕張中 角度の和 算数星人のweb問題集 中学受験算数の問題に挑戦
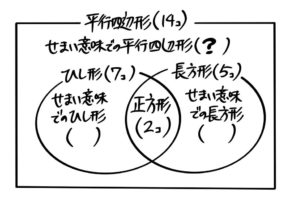



作成中 中学受験 四角形のまとめ 分類 公式から等積変形まで そうちゃ式 受験算数 2号館 図形 速さ
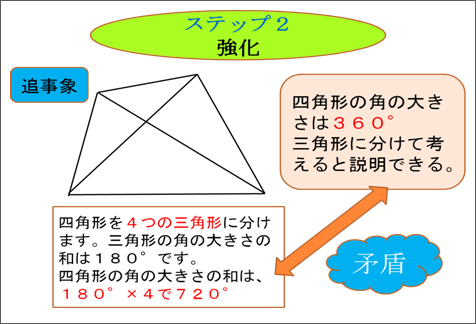



重なる形と図形の角を調べよう 図形の角と合同 第5学年 小学校 算数 My実践事例 日本文教出版
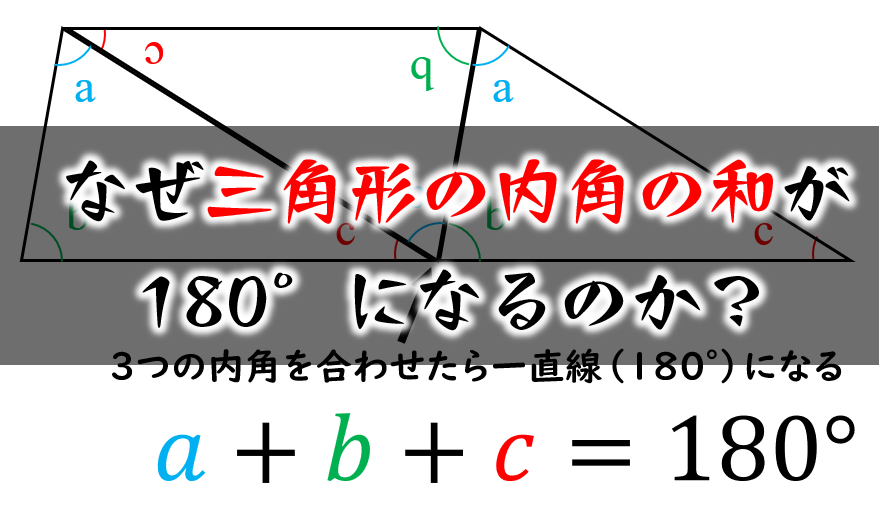



三角形の内角の和が180 なのはなぜ 小学生に教えるための解説 数学fun
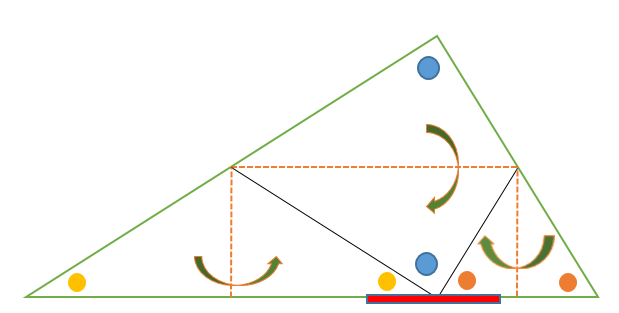



小学算数 幼稚園児でもわかる 三角形の内角の和 180度 の証明 偏差値40プログラマー
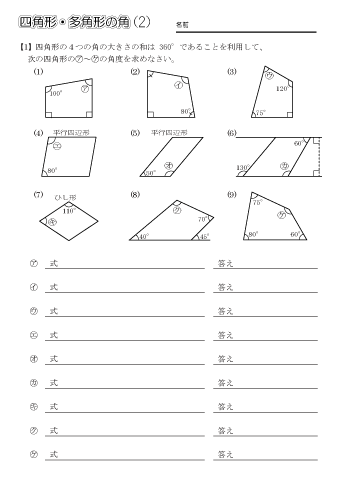



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生
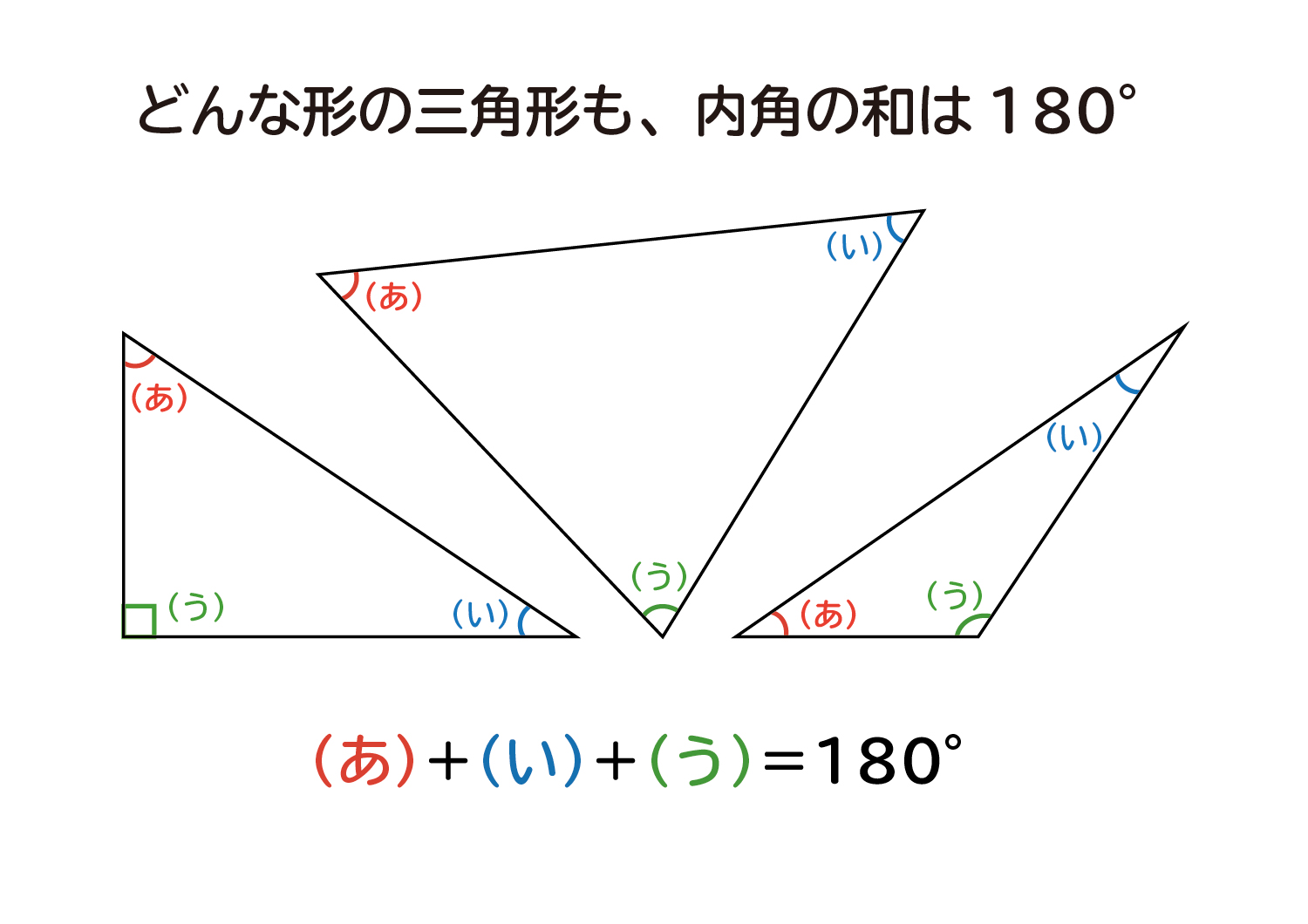



なぜ 三角形の 内角の和は180 なのか を説明します おかわりドリル




フレッシュ ひし形 書き方 コンパス
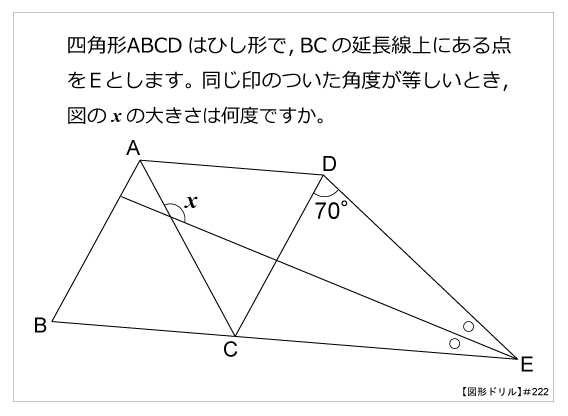



図形ドリル 第222問 ひし形と二等分線 算数星人のweb問題集 中学受験算数の問題に挑戦



0 件のコメント:
コメントを投稿