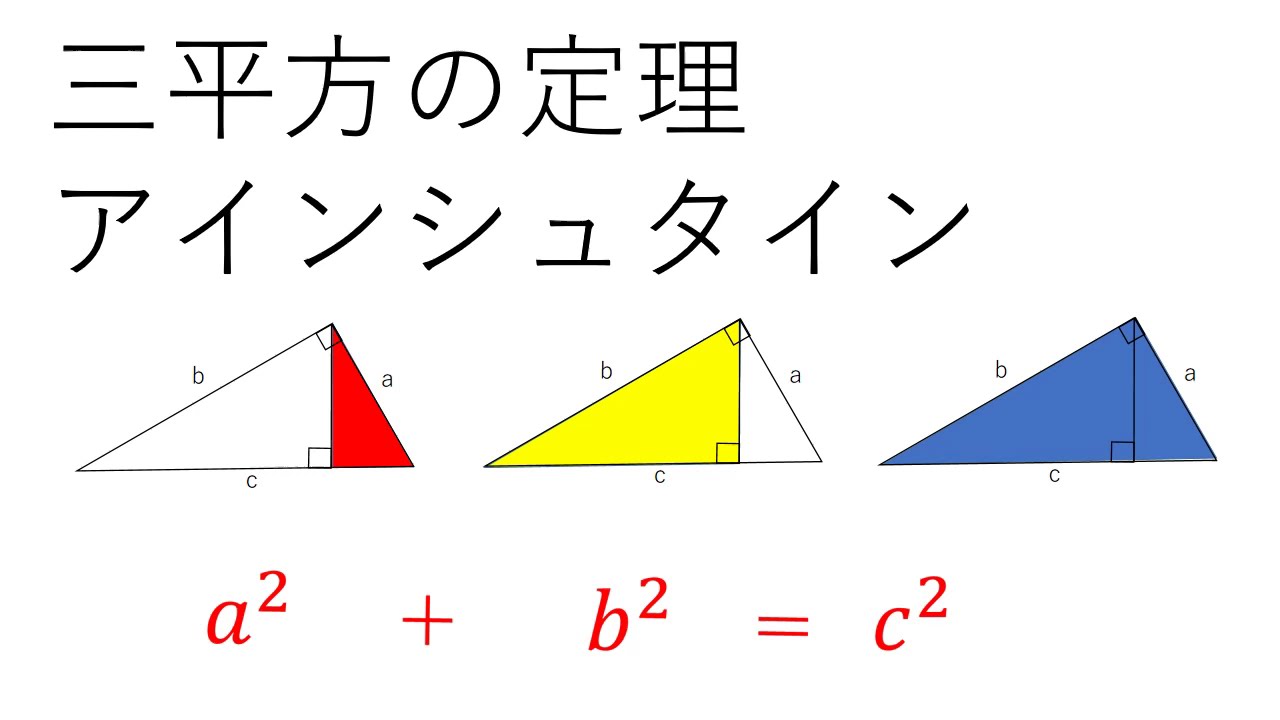
三平方の定理
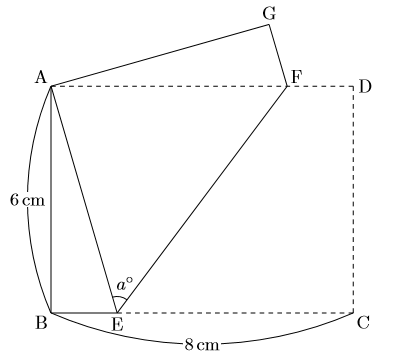
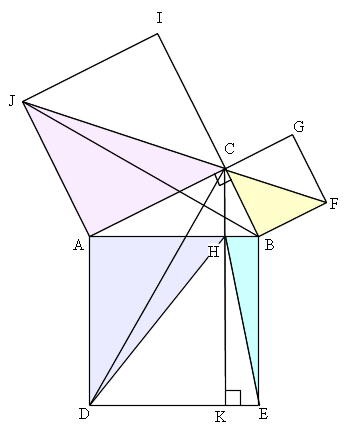
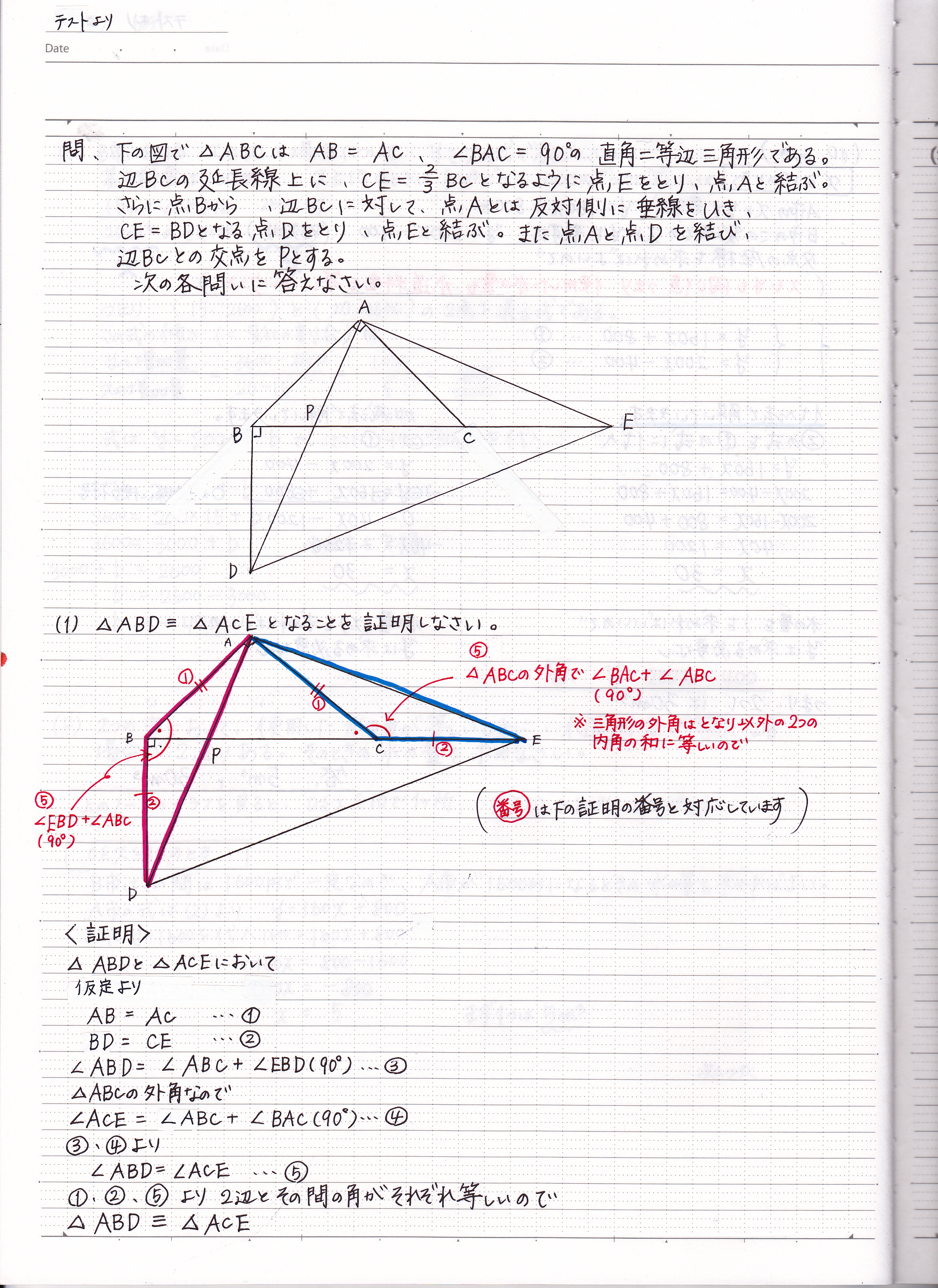
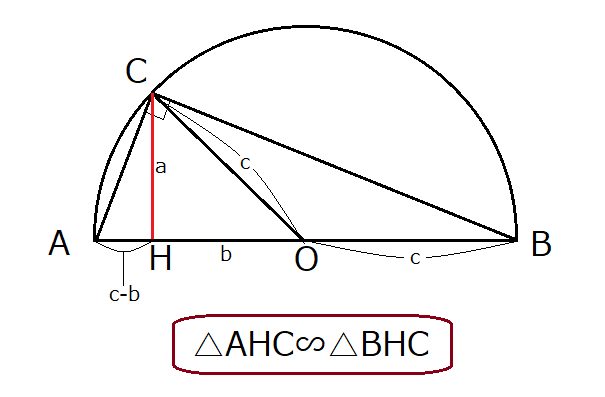
adeで三平方の定理を使って、 ac²=ad²dc² ac²=816=24 ac>0より、 ac=2√6 と求まります。 まとめ いかがでしたか? 個人的には2つ目のやり方が分かりやすいように思っています。 他にもいろいろなやり方がありますのでぜひ探してみてください。三平方の定理 発展問題まとめ お疲れ様でした! 入試などの発展問題では、今回のように 三平方の定理を使って、方程式を作ることで 長さを求めていくようになります。 まずは、求めたい部分を とする。 直角三角形の各辺を を使って表すことが
三平方の定理 証明 面白い
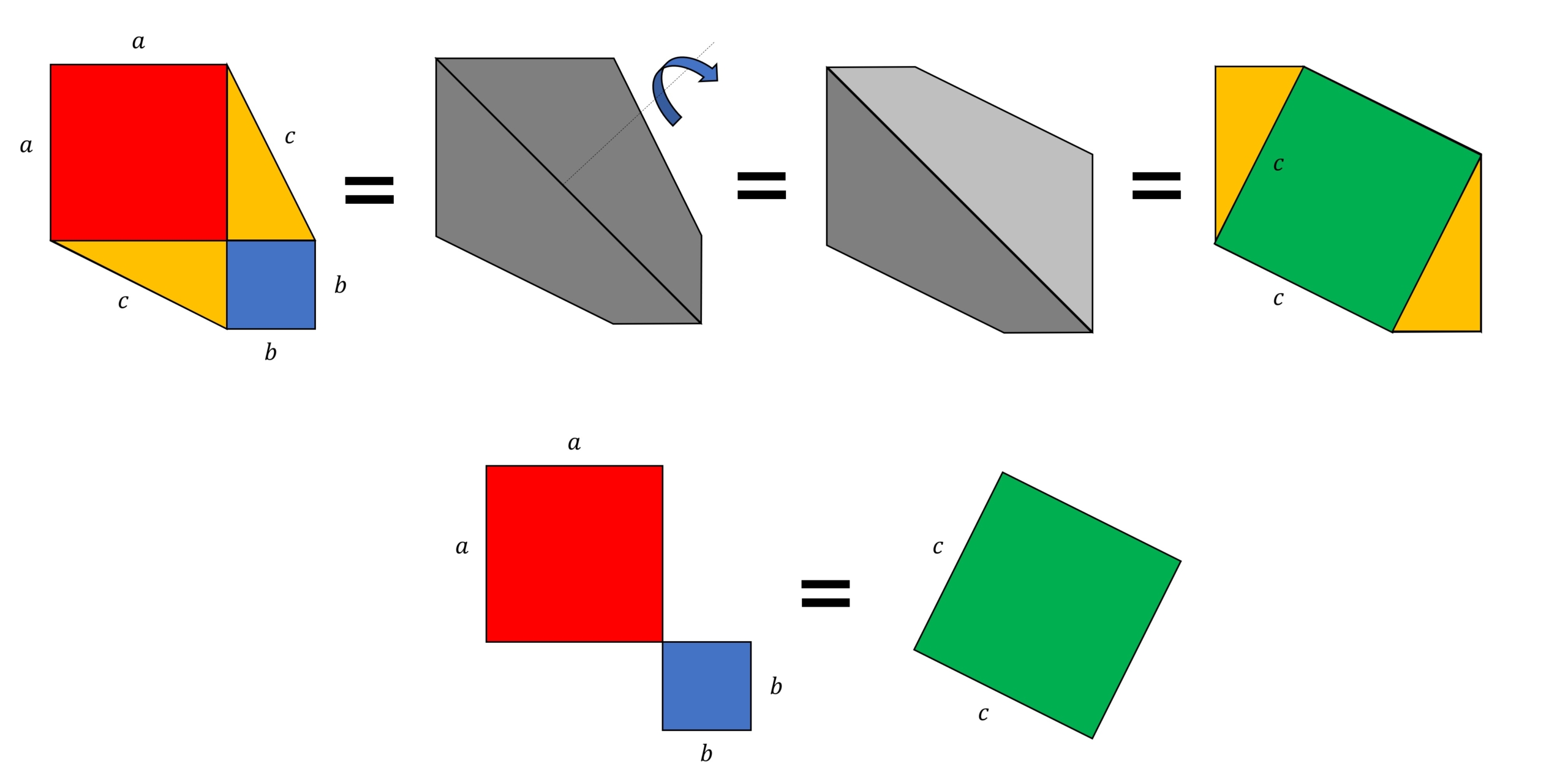
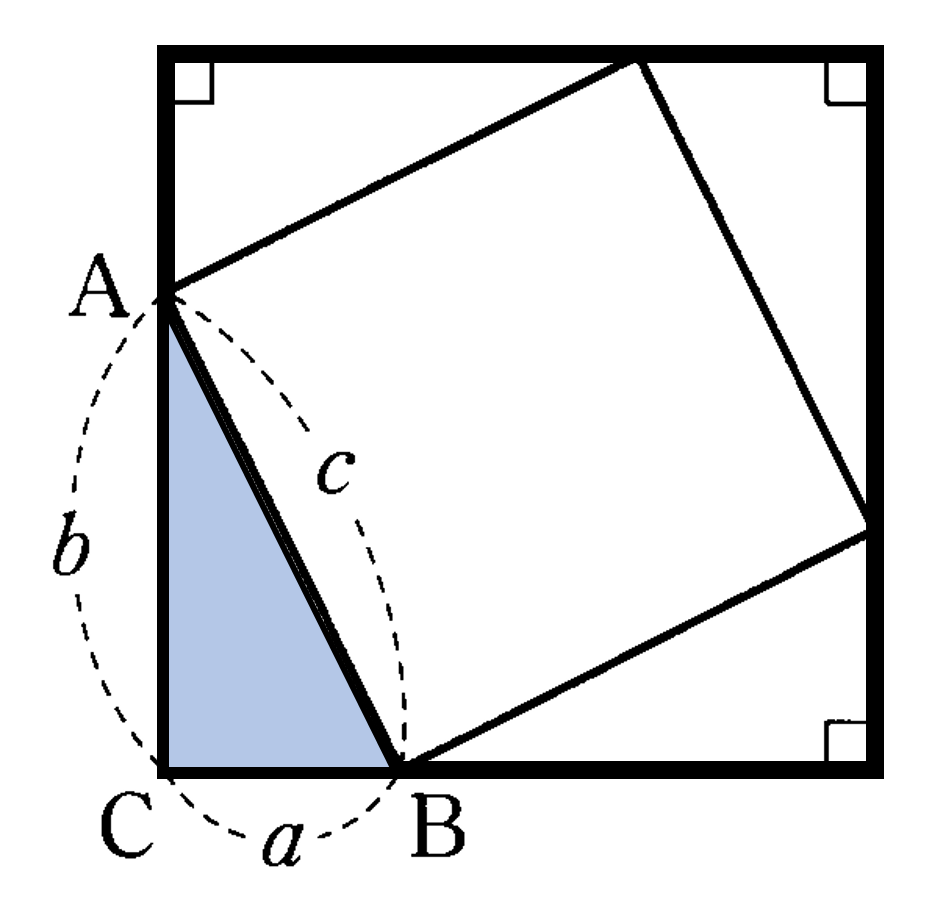
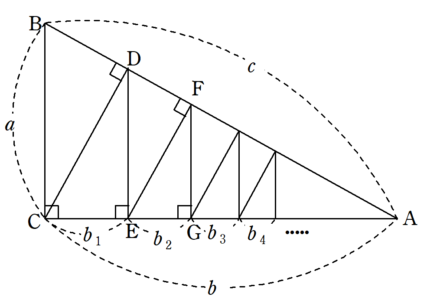
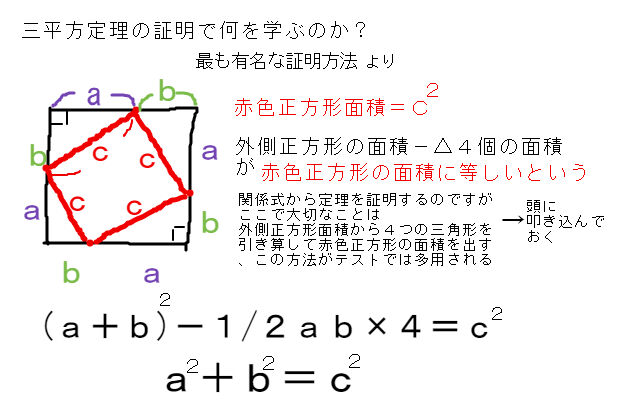
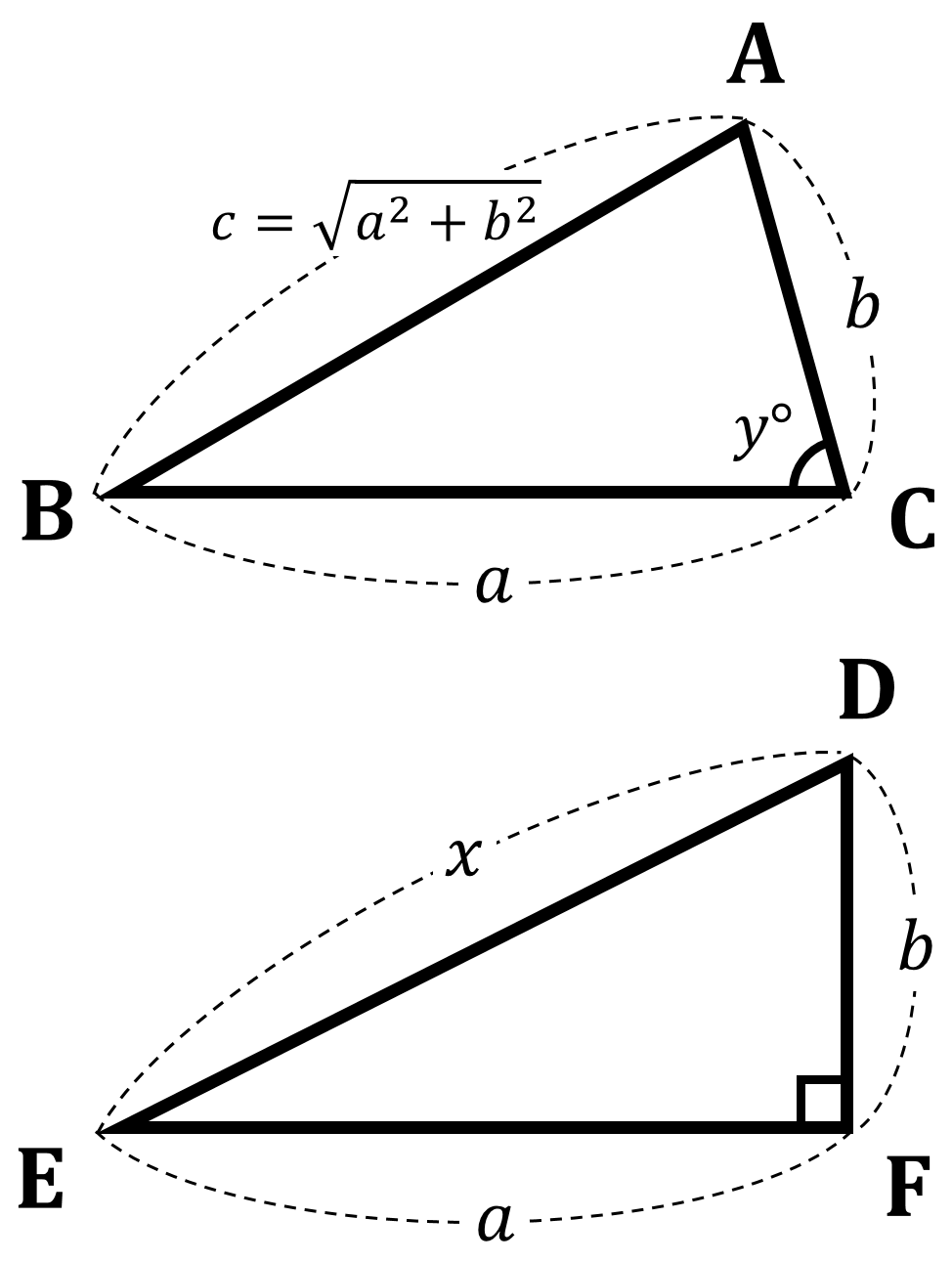
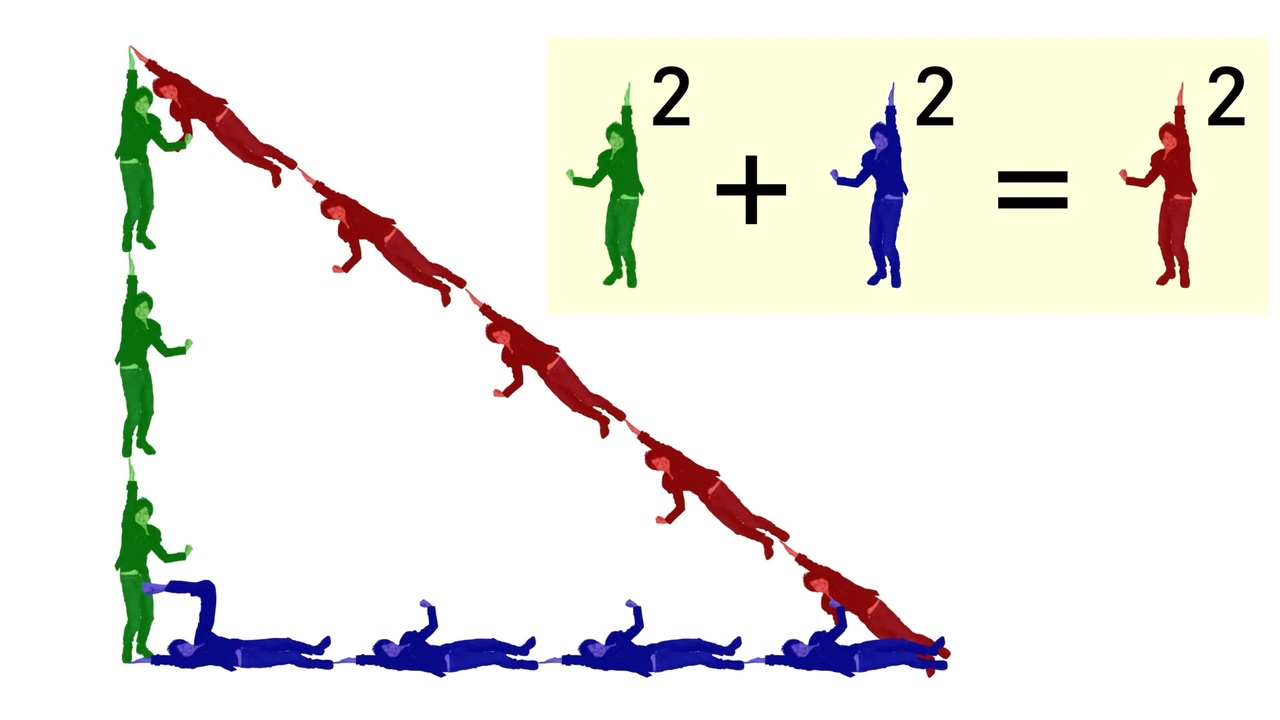
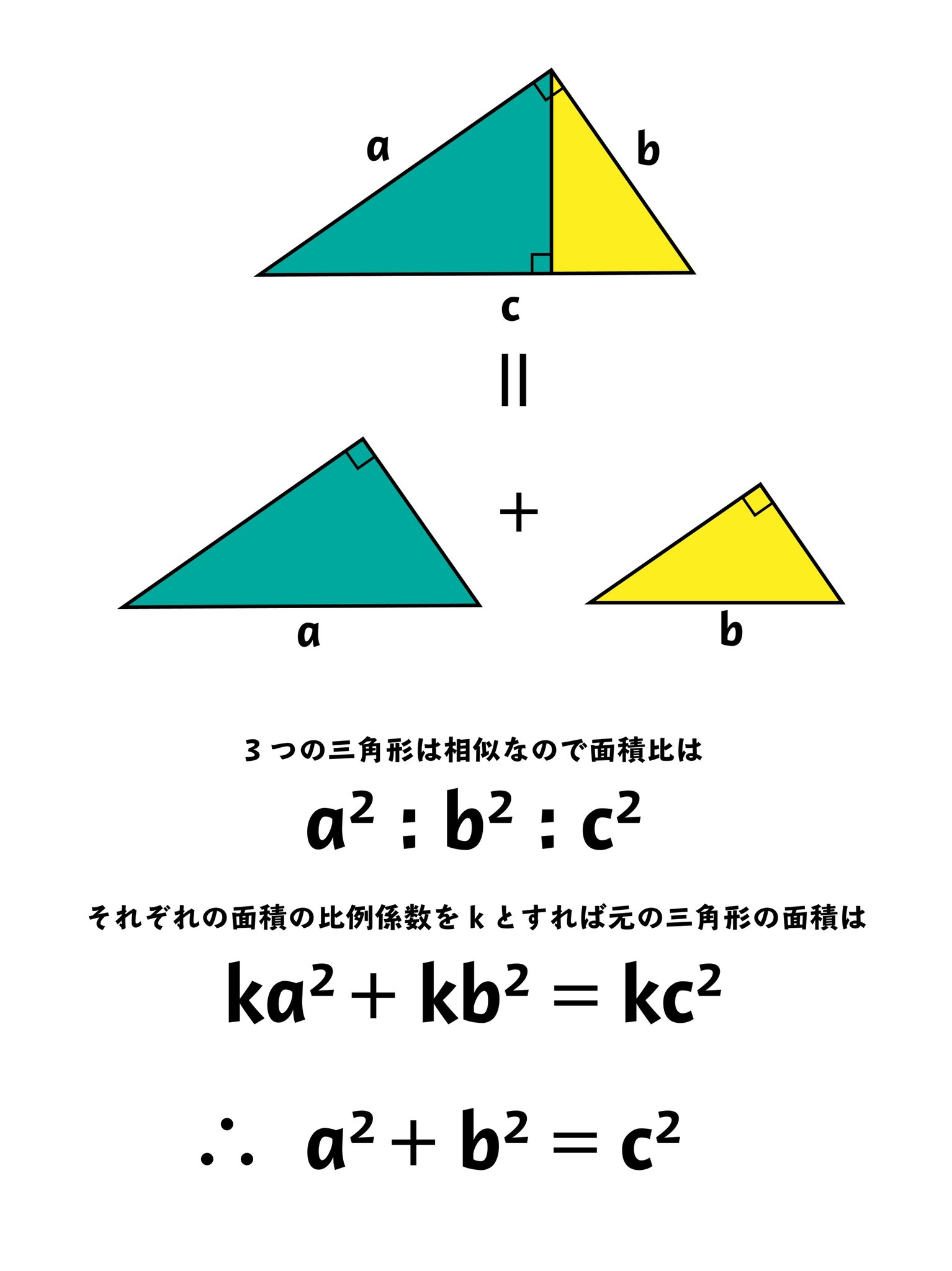
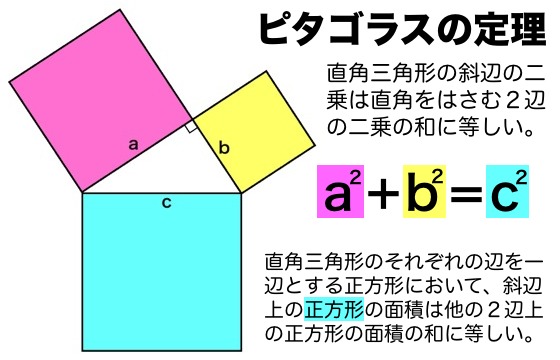
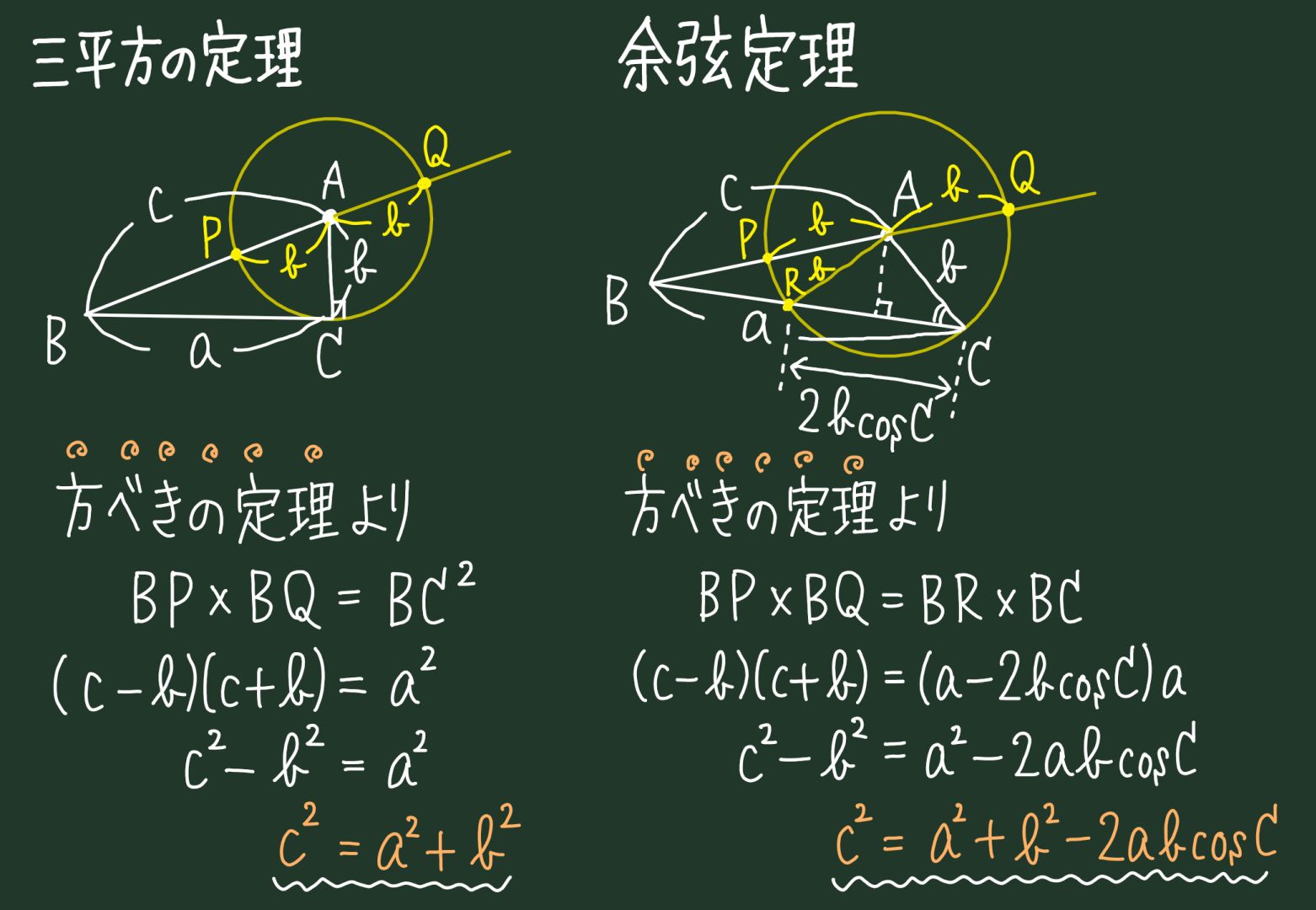
三平方の定理 証明 面白い- 三平方の定理の証明 三平方の定理とは以下のように直角三角形ABCがあった時に、辺a(底辺)と辺b(高さ)の2つと辺c(斜辺)の関係性を以下のような等式で表した定理です。 公式:a²+b²=c² わかりやすく文章で表現しますと、 底辺の2乗と高さの2乗の 三平方の定理の証明は、紀元前からあらゆる人があらゆる方法で考え出してきました。 この記事では、三平方の定理の証明の中では珍しい、 無限を用いた証明方法 を、 現役数学教員がわかりやすく解説 します。 直角三角形を無限に細かくし、最終的に無限等比数列を利用する方法 。
三石 数学塾 三平方の定理の証明
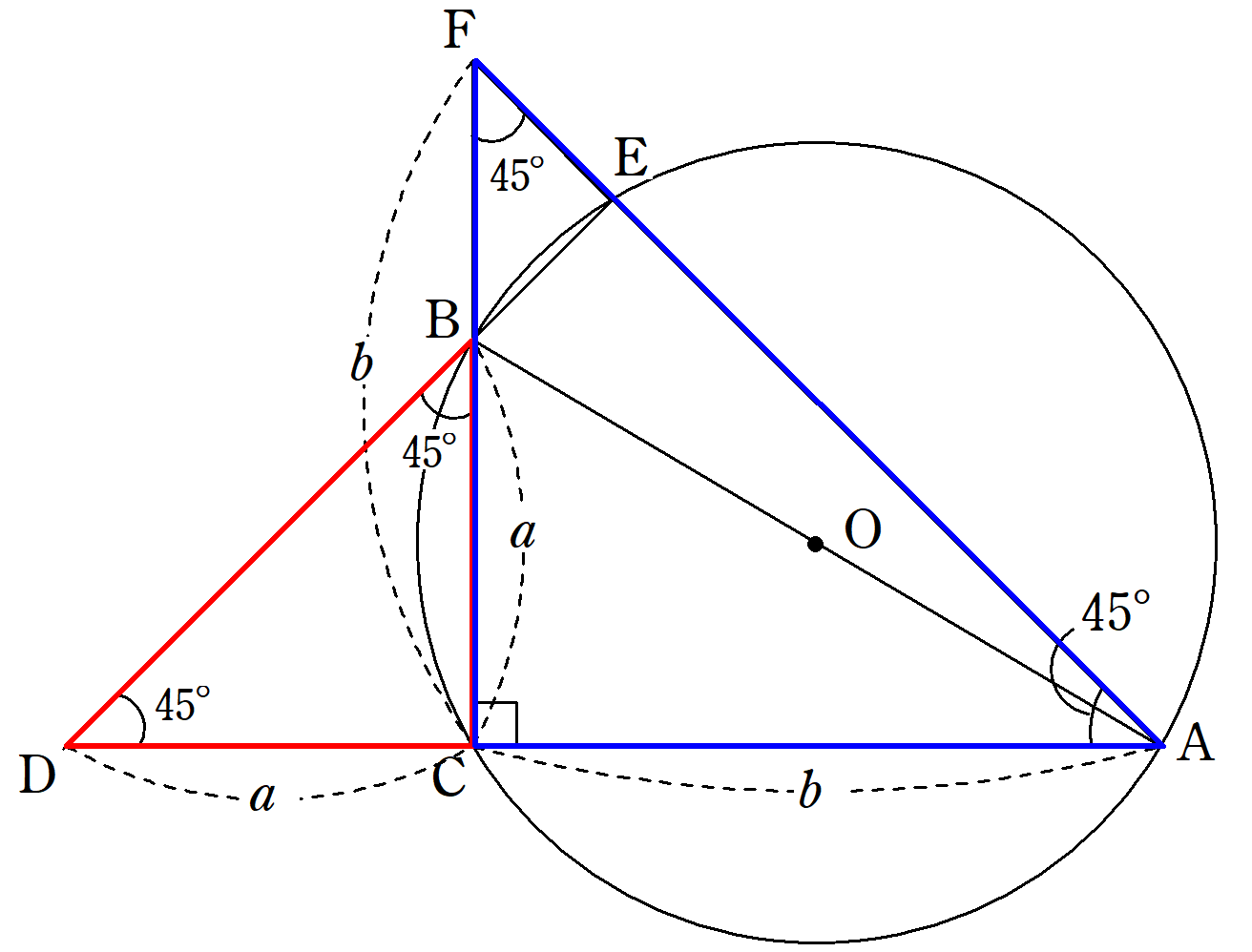
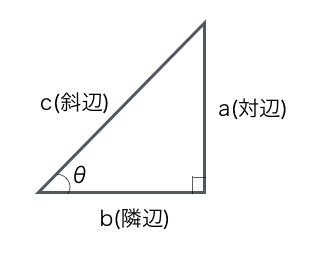
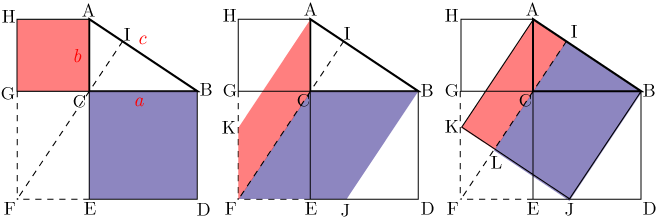
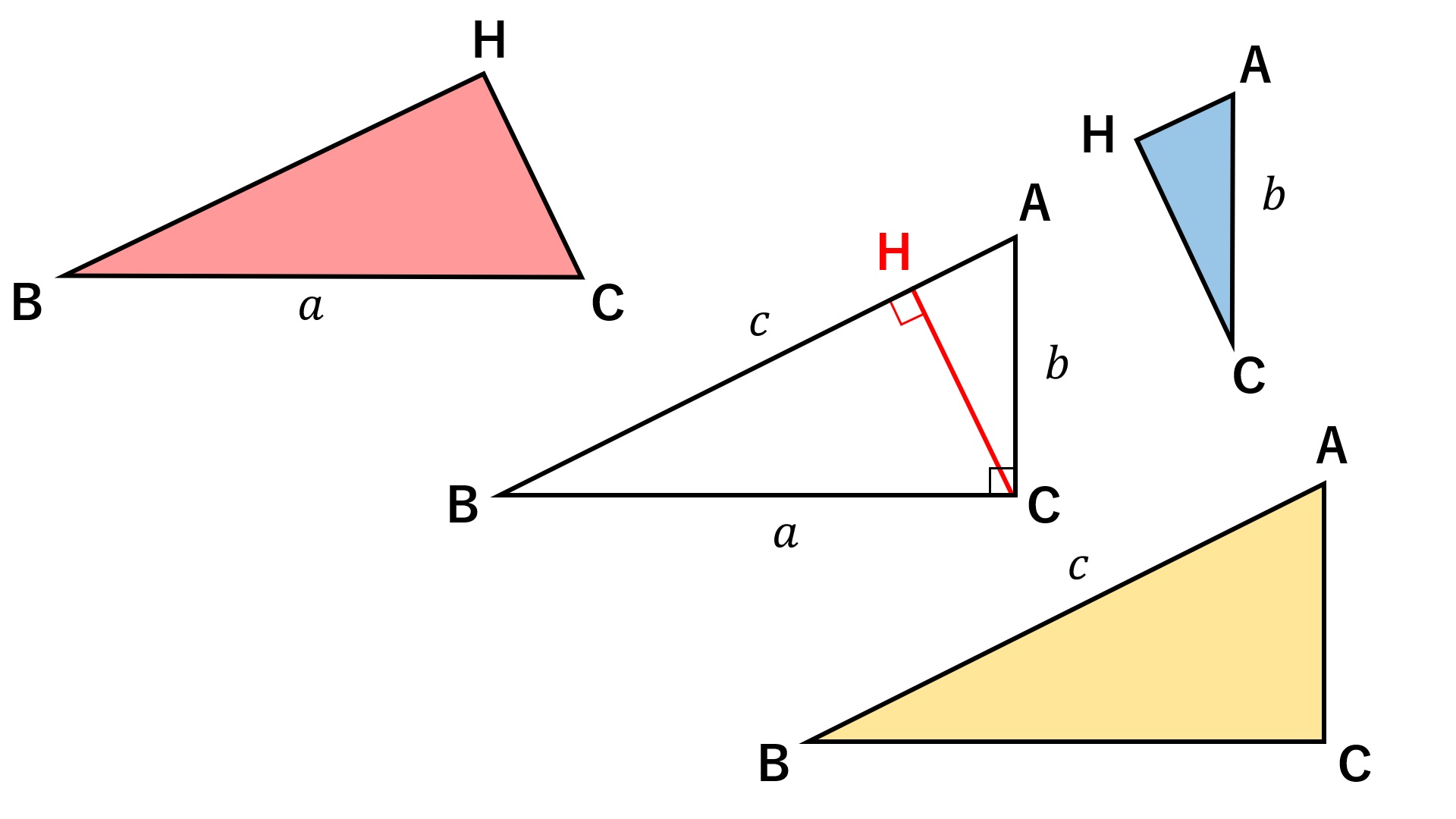
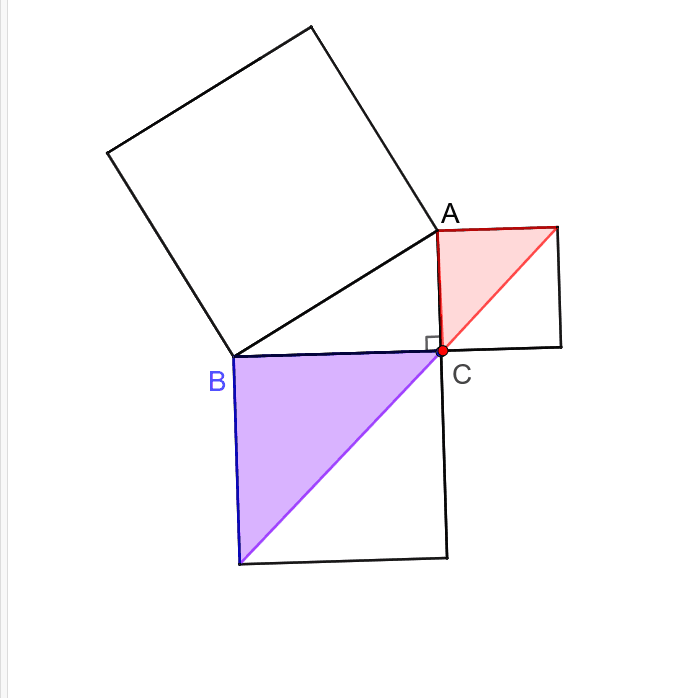
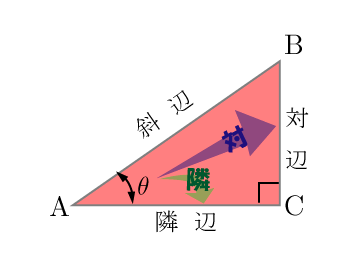
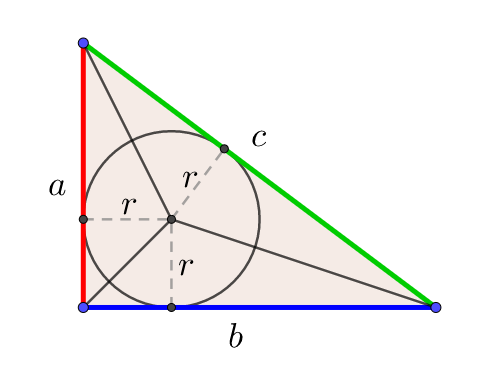
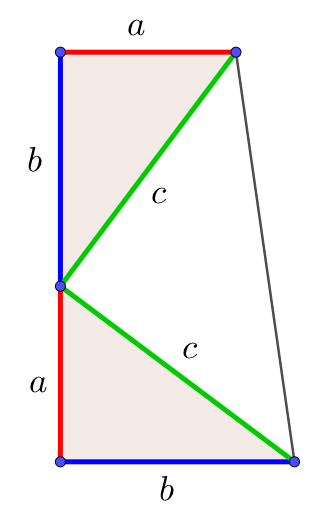
この直角三角形は,もとの直角三角形ABCをc倍したものになる。 ゆえに、cc=aabb よって、c 2 =a 2 b 2 この証明を見たときには,こんなに面白い(変わった?)証明の仕方もあるのかと思いました。 三平方の定理の変わった証明の方法を知っていれば,お教え下さい。数学史から入る「三平方の定理」 「三平方の定理」は,いつ,どのようにして発見されたか ・・・・・・ 片野 善一郎;三平方の定理とは? 三平方の定理とは、古代ギリシアの数学者である「ピタゴラス」の名前を取って、「ピタゴラスの定理」と呼ぶこともある定理で、「直角三角形の3辺の長さの関係」表す定理です。 直角三角形とは、中学数学で散々見てきた これですね。
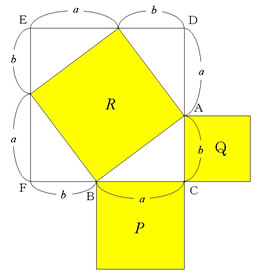
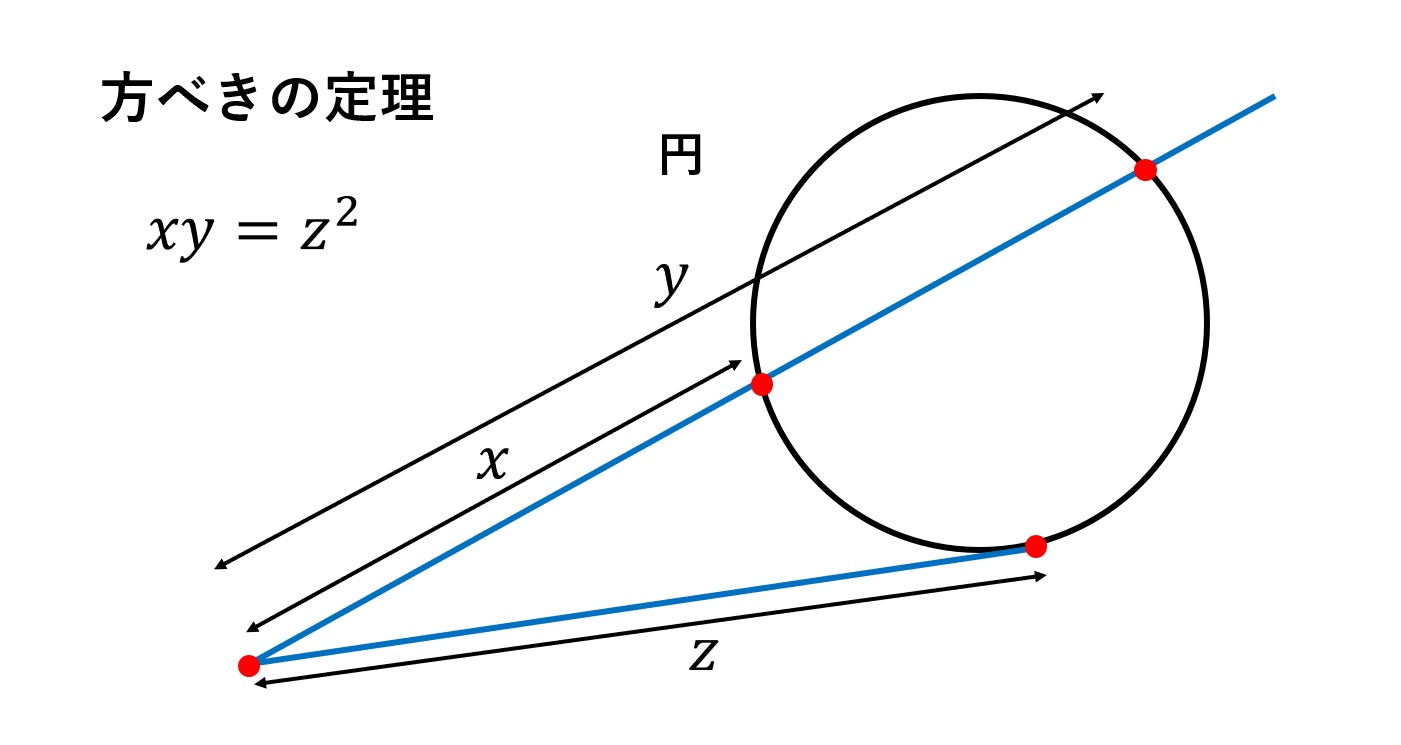
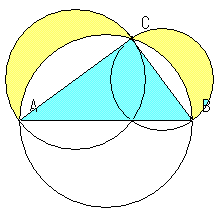
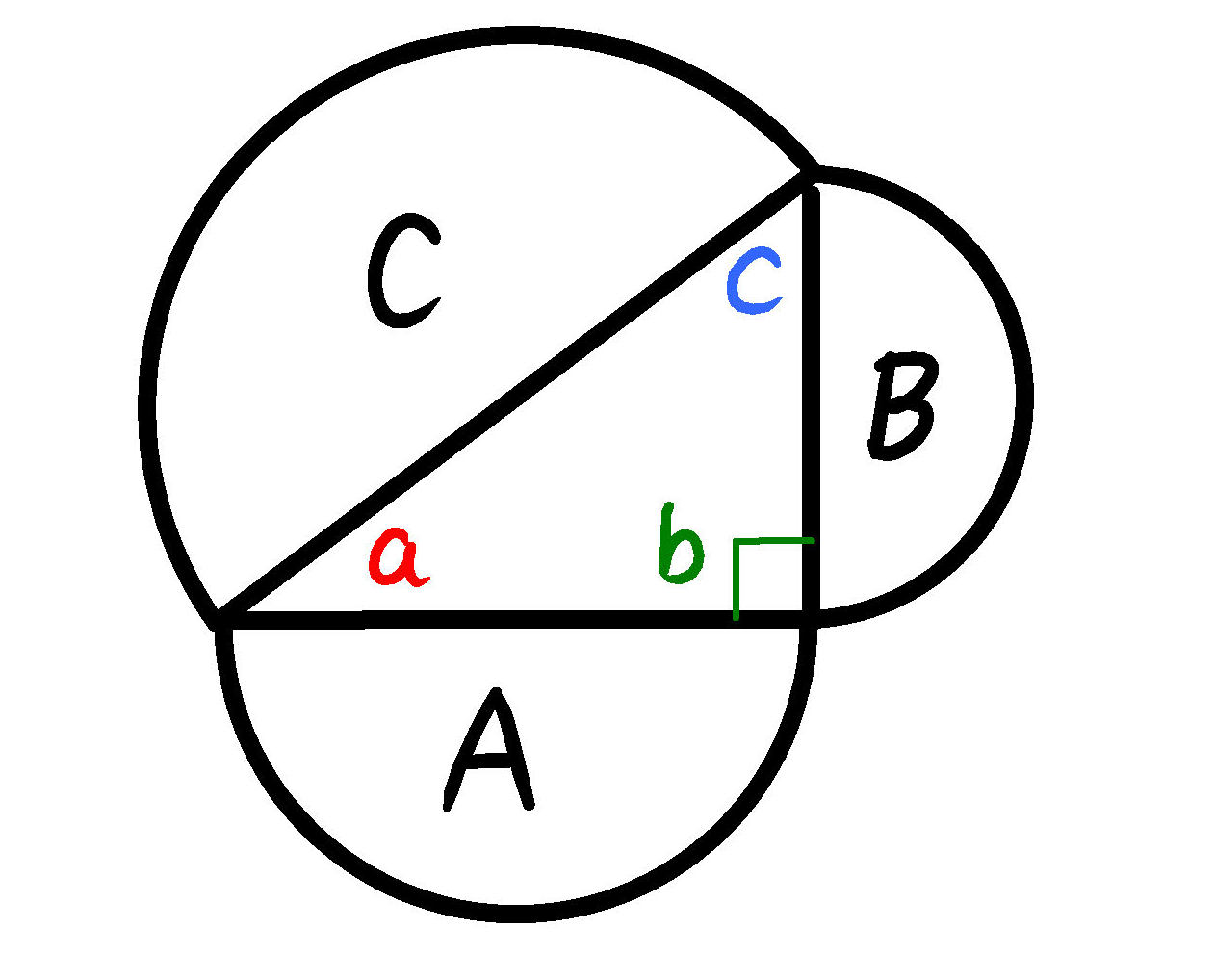
三平方の定理がひと目で分かる展示が面白い 年5月日 こんにちわスピカです。 小学校のころに習った三平方の定理ってやつ覚えています。 そう直角三角形の斜辺の2乗は隣辺の2乗と対辺の2乗の和に等しい。 というやつ。 あれって公式があった a2 「三平方の定理」がひと目で分かる展示が面白いと話題に 「視覚的にわかる」「こういうのが学校にあったら」|数学 液体の動きで見るとよりワクワクできます中学生の頃に習った「三平方の定理」がひと目で分かる展示が「面白い」「すごい」とTwitterで話題です・・・ 引用元nlabitmediaco a2b2 = c2 a 2 b 2 = c 2 ですが四平方の定理だと, S2 = S12S22 S32 S 2 = S 1 2 S 2 2 S 3 2 となります. ここでS はそれぞれの三角形の面積です.また, ABC以外は全て直角三角形です. 三平方の定理では線分の長さでしたが四平方の定理では各三角形の面積を
三平方の定理 証明 面白いのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  |  |
「三平方の定理 証明 面白い」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「三平方の定理 証明 面白い」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「三平方の定理 証明 面白い」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三平方の定理 証明 面白い」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三平方の定理 証明 面白い」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「三平方の定理 証明 面白い」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「三平方の定理 証明 面白い」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「三平方の定理 証明 面白い」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「三平方の定理 証明 面白い」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
「三平方の定理 証明 面白い」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「三平方の定理 証明 面白い」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
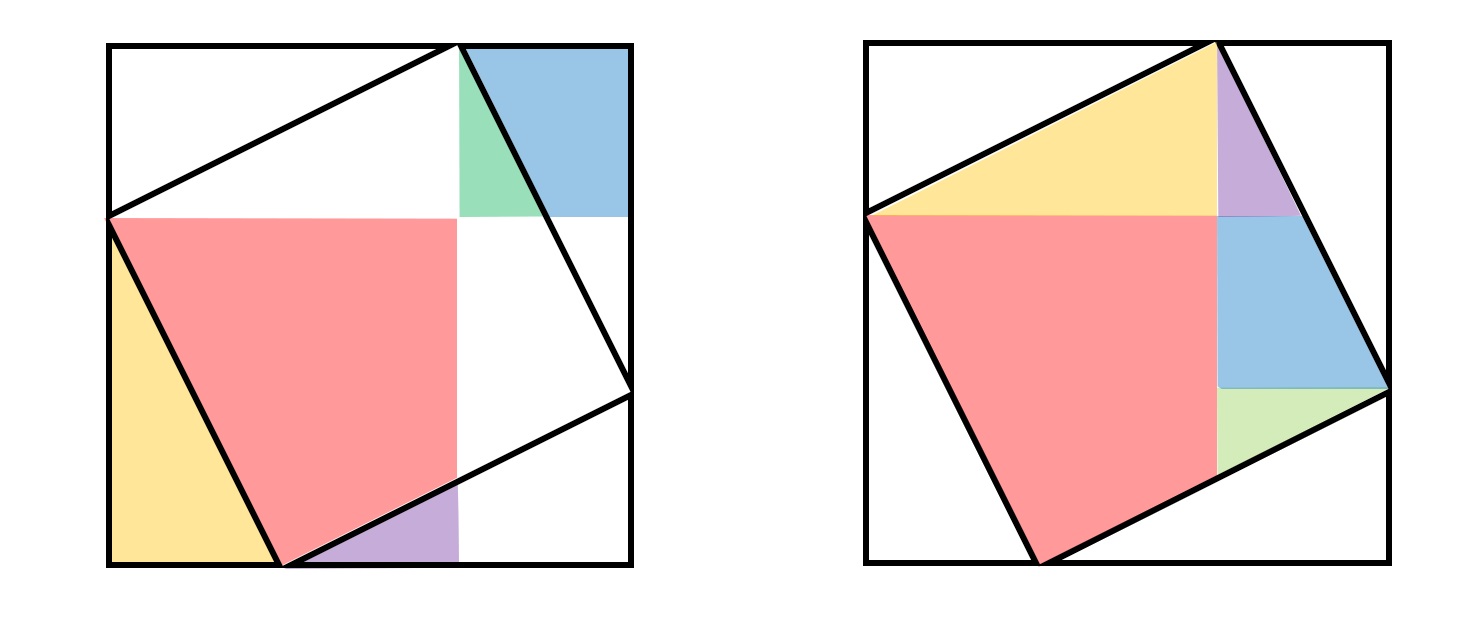
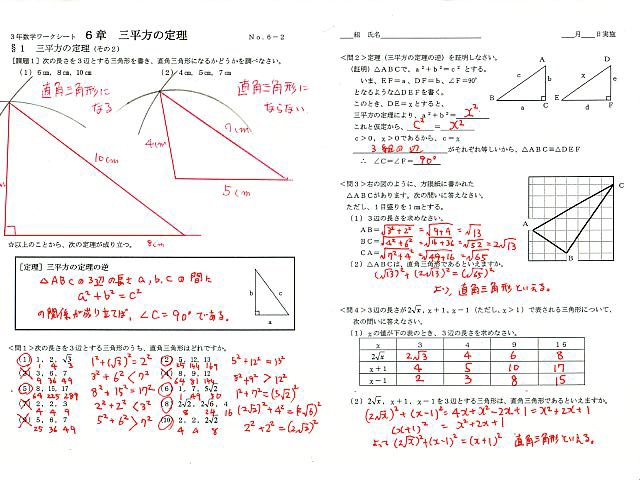
ここまでくると、もう立派な三平方の定理です。 (4) 三平方の定理の証明 「どんな直角三角形でもa 2 +b 2 =c 2 であることを証明しよう。」これまでに、やったことを使って証明します。 どの考え方を使うのかを、最初に決定させます。最近の投稿 確率のおもしろいお話! 三平方の定理(平面) Ⅱ 相似と線分比;
Incoming Term: 三平方の定理 証明 面白い,




0 件のコメント:
コメントを投稿